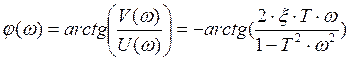Исследование характеристик контура стабилизации угла крена моделированием

;

и логарифмическую амплитудную характеристику:

.

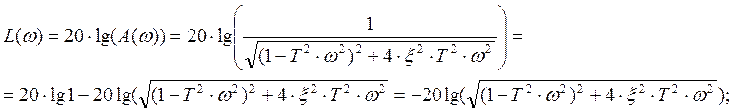
ЛАХ и асимптотическая ЛАХ  инерционного и колебательного звеньев представлены на рис. 3.2.2:

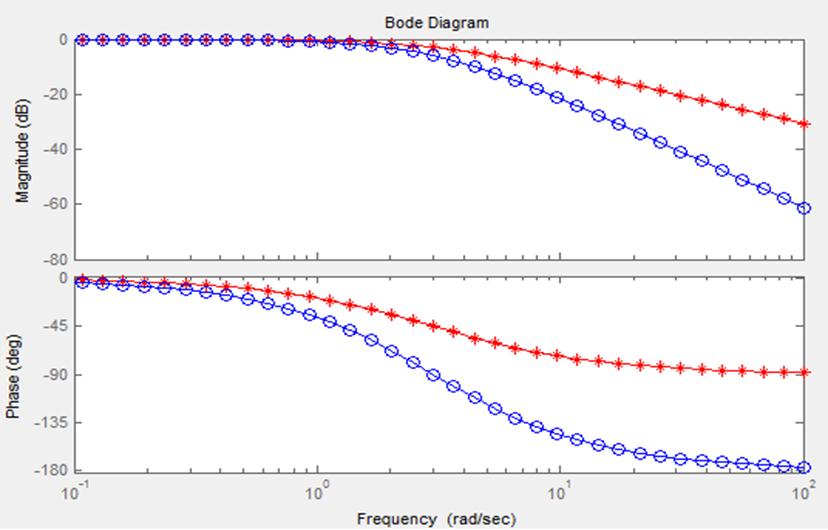
Рис. 3.2.2. ЛАХ и асимптотическая ЛАХ.

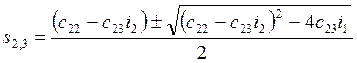
S₂=-0.611   S₃=-28.789

Если второй и третий корни представляют собой пару комплексно сопряженных корней, т.е. , где 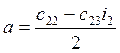 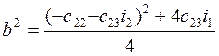 , то левую часть характеристического уравнения можно записать в виде:

.

В этом случае

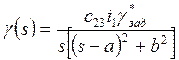.                         (3.3.8)

Из таблиц изображений по Лапласу выбираем формулу, соответствующую выражению (3.3.8):

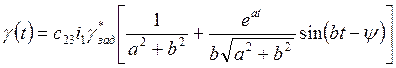,                                      (3.3.9)

где.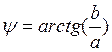

Аналогично определяем 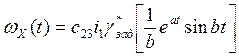   .                        (3.3.10)

Если корни  и  являются вещественными как в нашем случае

, то: 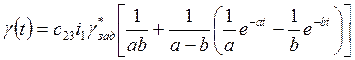 ,                   (3.3.11)

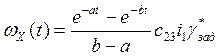.                                                                              (3.3.12)

В качестве конечного времени  следует принять такое время, когда переходные процессы закончились, и изменение величин  пренебрежимо мало.

Результаты расчетов  сводятся в таблицу3.3.1.

Таблица 3.3.1:

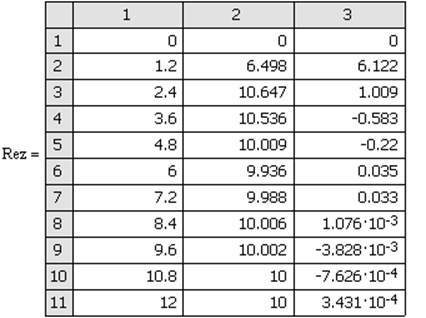
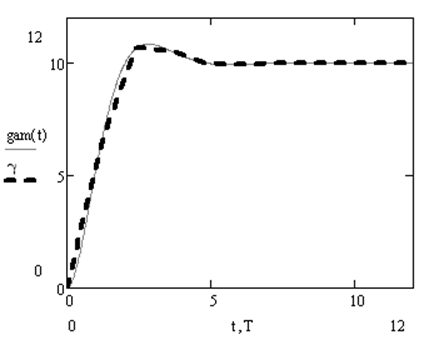
По данным таблицы 3.3.1 построены графические зависимости, представленные на рис.3.3.1 и рис. 3.3.2.

Моделирование.

 Исследование характеристик контура стабилизации угла крена моделированием проводится с помощью программы Gamma (Приложение 2).Результаты реализации программы представлены на рис. 3.3.3 и рис.3.3.4.

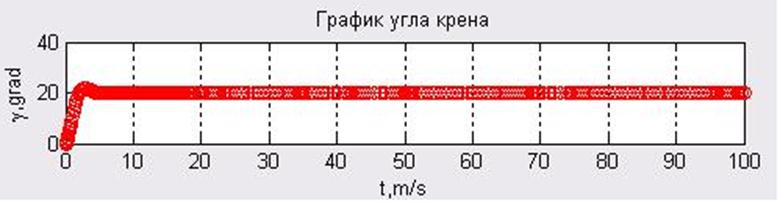
Рис. 3.3.3. Зависимость угла крена от времени.

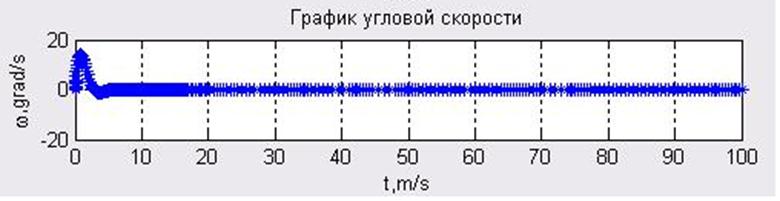
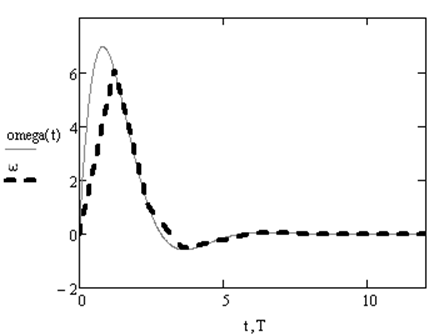
Рис. 3.3.4. Зависимость угловой скорости от времени.

Показатели качества и точности системы стабилизации угла крена:

1.  Время переходного процесса  10 секунд .   

2.  Перерегулирование .

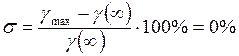3.  Время первого выброса – нет.

4.  Колебательность, определяемая числом колебаний за время переходного процесса – 0 колебаний.

5.  Затухания за период – нет.

6.  Установившееся значение ошибки: .

Запишем матрицу коэффициентов Гурвица : .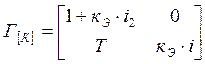

Система устойчива, если все главные определители матрицы Гурвица больше нуля.

;

.

 - больше нуля, следовательно, исследуемая система стабилизации угла крена устойчива.

 Исследование устойчивости по критерию Михайлова.

  Для определения устойчивости по критерию Михайлова записывается характеристический полином замкнутой системы:

.

Подставляя , получаем .

Выделяем мнимую и действительную части:

,   .

Данные вычисления , при изменении  от 0 до ¥ представлены в таблице 3.4.1.

Таблица 3.4.1:

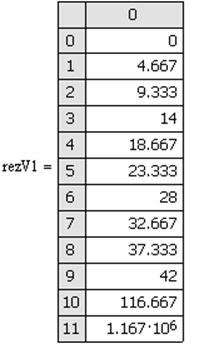
По данным таблицы 3.4.1 на комплексной плоскости строится годограф Михайлова.

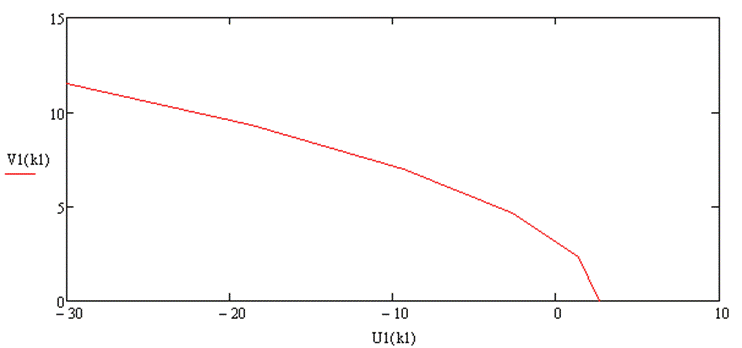
Кривая Михайлова последовательно проходит 2 квадранта, все время, окружая начало координат, в положительном направлении, следовательно, исследуемая система устойчива.

Исследование устойчивости по критерию Найквиста.

Для определения устойчивости по критерию Найквиста определяется передаточная функция разомкнутой системы:

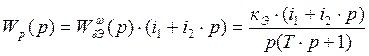 .  (3.4.4)

Частотная характеристика разомкнутой системы имеет вид:

.

Для нахождения мнимой  и действительной  частей подставим в формулу (3.4.4) . Получим:

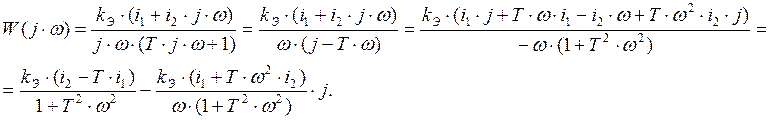
Отсюда имеем:  ,  .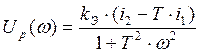

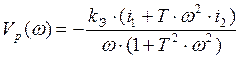Данные вычисления , при изменении  от 0 до ¥ представлены в

таблице 3.4.2.

Таблица 3.4.2:

По данным таблицы 3.4.1 на комплексной плоскости строится график амплитудно-фазовой характеристики разомкнутой системы, представленный на

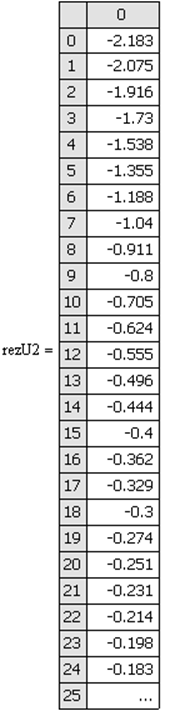
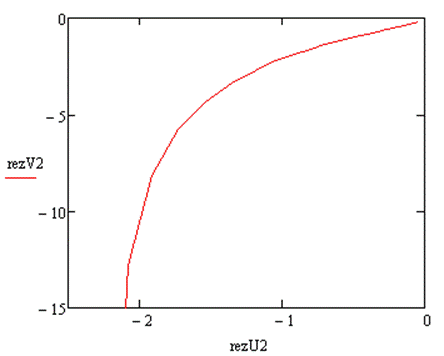
Рис. 3.4.2. Амплитудно-фазовая характеристика разомкнутой системы.

Кривая на рис. 3.4.2 не охватывает точку на комплексной плоскости , следовательно замкнутая система устойчива, согласно критерию Найквиста.

Построение областей устойчивости в плоскости параметров автопилота на основе метода D - разбиений.

Системы стабилизации угла рыскания имеет вид:

.

Приравнивая к нулю вещественную и мнимую части, получим два уравнения для определения :

.

Для решения этой системы воспользуемся правилом определителей; определитель системы равен:

.

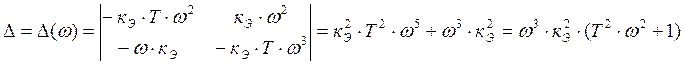Определители, соответствующие , равны:

,

.

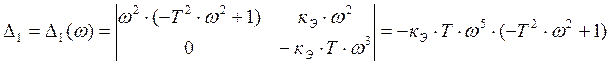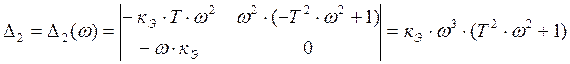Решение системы имеет вид:

,

.

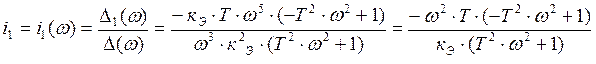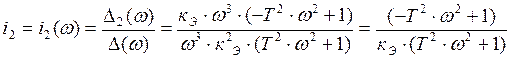Последние два уравнения представляют собой уравнения D - кривой в параметрической форме.  Для построения D – кривой параметр  изменяется от -до +. D – кривая штрихуется слева при увеличении , если определитель системы  больше 0, и справа, если определитель системы  меньше 0. при этом ось  - абсцисс, - ординат.

D-кривая представлена на рис.3.4.3. Штриховкой показана область устойчивости.

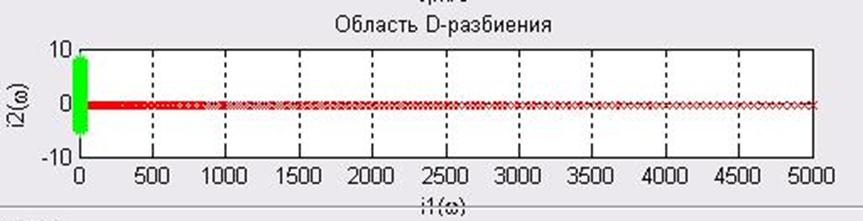
Рис. 3.4.3. D-кривая и область устойчивости.

Список использованной литературы.

1. А.С. Шалыгин, С.А. Кабанов, О.А. Толпегин. Расчет динамических характеристик систем автоматического управления на ЭВМ. Лабораторный практикум. Ленинград, 1986г.

2. А.С. Шалыгин, В.А. Бородавкин, В.А. Зазимко, В.А. Петров, В.А. Санников,

О.А. Толпегин. Анализ и синтез законов управления систем стабилизации беспилотных летательных аппаратов методами моделирования. Санкт-Петербург, 2005.

3. И. Л. Петрова, А. Н. Пономарев. Исследование динамики линейных систем управления беспилотных летательных аппаратов. Лабораторный практикум. [Электронный ресурс]. Санкт-Петербург, 2008. http://lib_server/elres/elr00971.pdf.

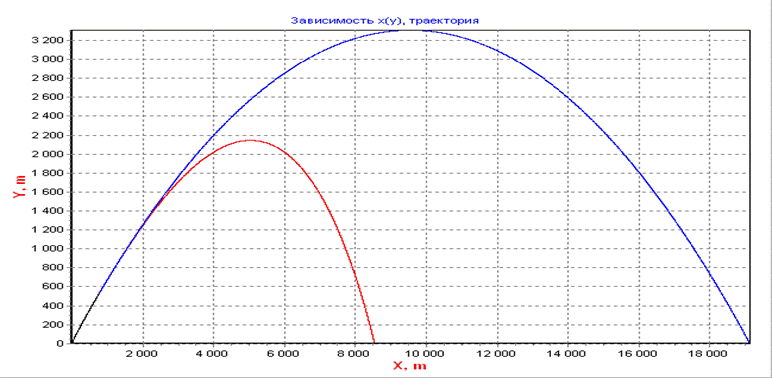
Результаты расчетов представлены в сравнении с расчетами реальной траектории в таблице.

точка	Координата Х, м (прог./параб.теория)	Координата Y, м (прог./параб.теория)
А	691.94/	512.35 /
D	8987/	3140/
С	18313/	483.15/
Е	18005/	0/0

Графики.

График изменения высоты полета от времени

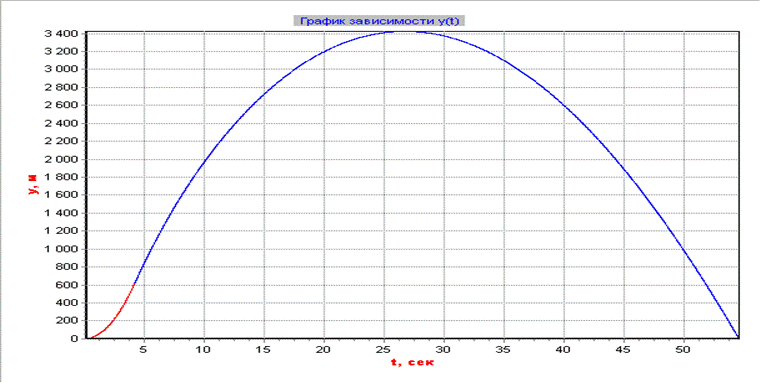
График изменения скорости полета в зависимости от времени на всем участке полета

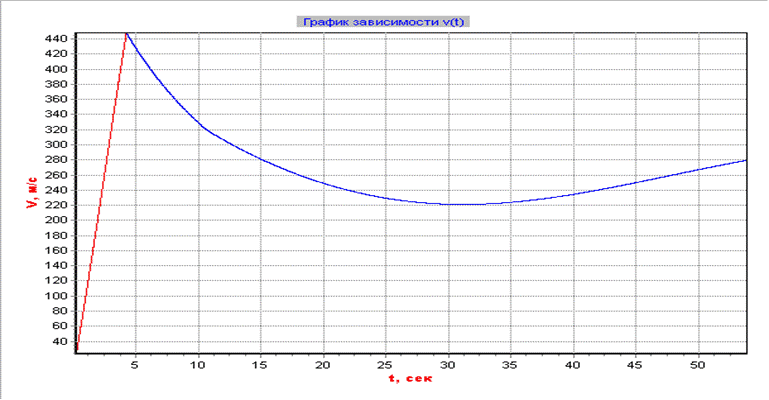
График изменения угла тета на всем участке полета

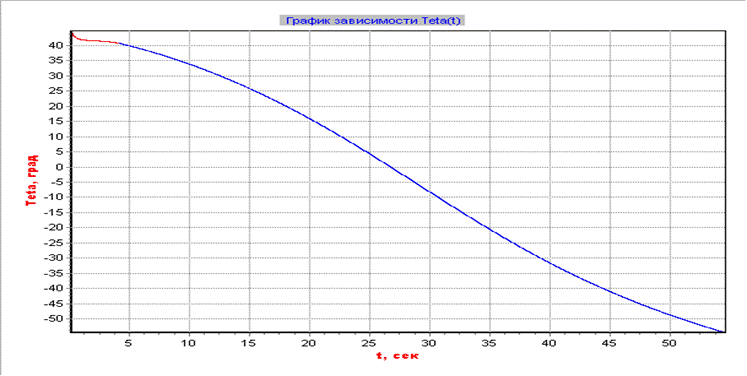
График изменения траектории на всем участке полета

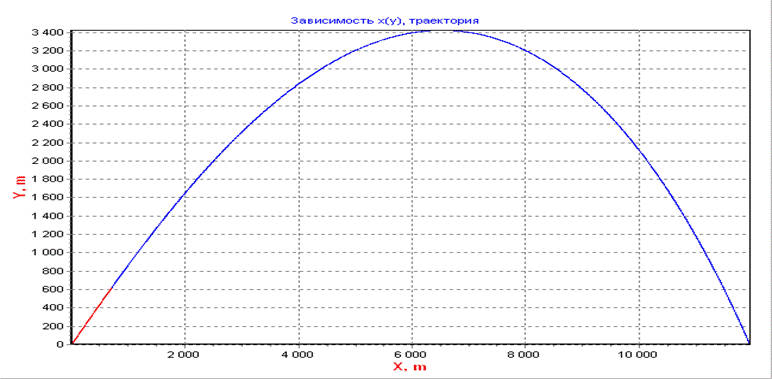
График траектории полета ракеты.