Составление математической модели полета неуправляемого летательного аппарата. Расчет дальности полета НЛА по параболической теории, страница 2

В усовершенствованном методе Эйлера – Коши в первом приближении полагается

, а во втором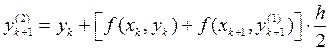

Погрешность метода Эйлера определяется остаточным членом ряда Тейлора 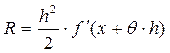, . Для обеспечения сходимости шаг h следует выбирать достаточно малым. Для метода Эйлера – Коши погрешность имеет порядок .

Активный участок траектории ЛА

 Расчет траекторных параметров на активном участке полета ЛА произведен с помощью программы eiler по математической модели приведенной в пункте 2.1. Решение системы дифференциальных уравнений производилось по методу Эйлера. Программа eiler  рассчитывает движение ЛА по направляющим без учета изменения массы ЛА, активный и пассивный участки траектории. При начале расчета активного участка траектории после схода с направляющих происходит скачкообразное изменение массы ЛА на величину израсходованного топлива за время схода с направляющих. Исходными данными для расчета являются исходные данные, приведенные в таблице 2.1. Так же в исходных данных задается шаг интегрирования, что позволяет варьировать точностью расчета в зависимости от задач расчета, оценочный расчет или уточненный.  

Проведем расчет одного шага интегрирования двумя способами: вручную и на ЭВМ с помощью программы eiler, для проверки правильности работы алгоритма расчета в программе eiler .

  Расчет вручную:

Начальными условиями для решения системы дифференциальных уравнений служат результаты расчета движения ЛА по направляющим, представленными в таблице 2.3.

1.  определение координат ЛА после схода с направляющих:

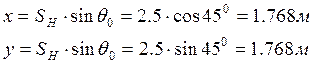
2.  определение координат ЛА с течением времени 0,001 сек:

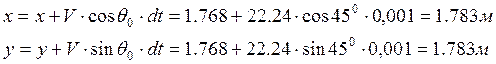
3. плотность на данной высоте - у:

, где r₀=1,23 кг/м³; 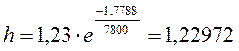 м

4. лобовое сопротивление при начальной (дульной) скорости:

5. определение   массы  ЛА  с  учетом   работы  ДУ  при  движении  по
направляющим:

 кг

      Н

6. Определение скорости полёта:

    

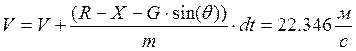
 7.  определение угла наклона траектории:

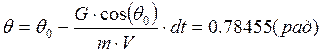
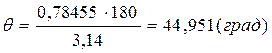
2.3 Расчет траектории реактивного снаряда по параболической теории.

Параболическая теория изучает движение тяжелой материальной точки в пустоте в однородном стационарном параллельном поле земного тяготения. Ее применяют для ориентировочного расчета траектории ЛА, имеющих большой вес и малую скорость полета, и для расчета траектории ЛА на больших высотах, где сила сопротивления ничтожно мала.

Основные формулы параболической теории:

1.

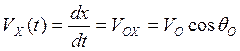
2.

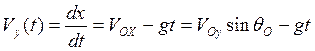
3.

4.

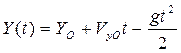
Здесь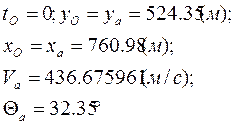  

 

Для вершины траектории (точка D) время вычисляется по формуле: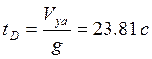

Поставляя  в формулы 3 и 4, получим:

Для точки Е (конец траектории) имеем . Тогда

откуда 

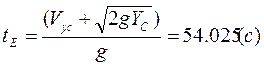
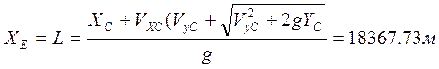
Точка Сявляется симметричной относительно точки А, следовательно высота .

Результаты расчетов представлены в сравнении с расчетами реальной траектории в таблице.

точка	Координата Х, м (прог./параб.теория)	Координата Y, м (прог./параб.теория)
А	691.94/	512.35 /
D	8987/	3140/
С	18313/	483.15/
Е	18005/	0/0

Графики.

График изменения высоты полета от времени

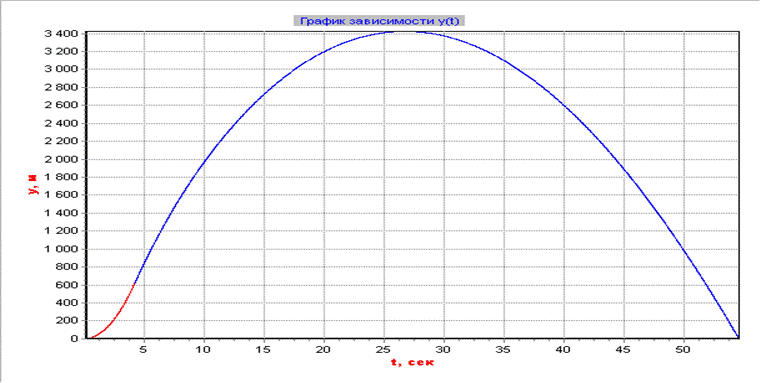
График изменения скорости полета в зависимости от времени на всем участке полета

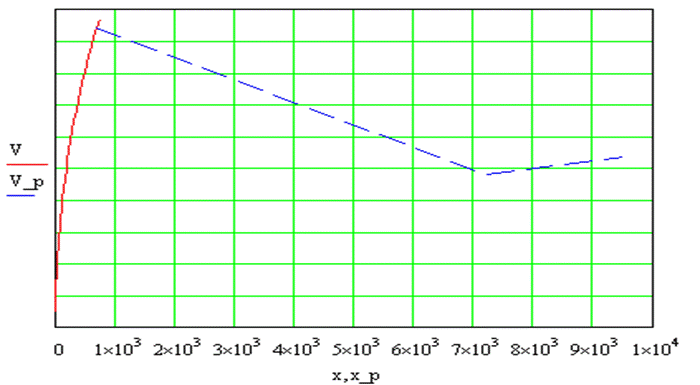
График изменения угла тета на всем участке полета

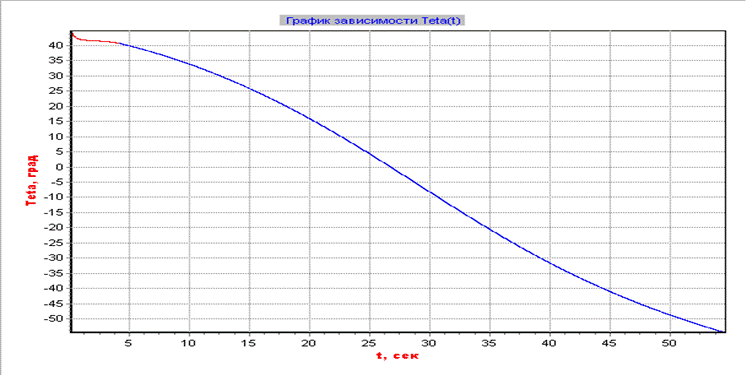
График изменения траектории на всем участке полета

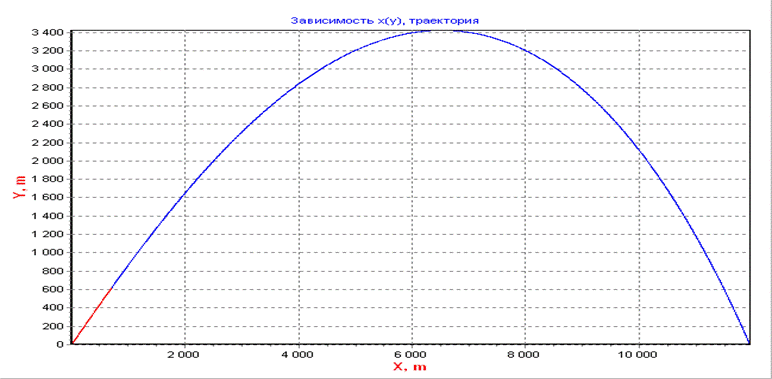
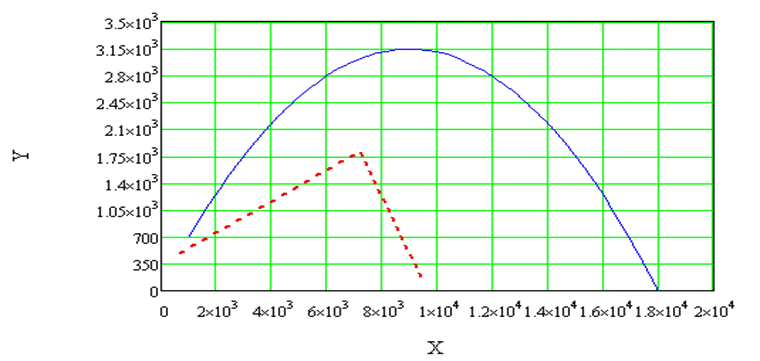
График траектории полета ракеты.

3. Исследование контура стабилизации угла крена беспилотного летательного аппарата.

3.1 Модель контура стабилизации угла крена в виде системы дифференциальных уравнений и структурной схемы.

  Рассмотрим систему стабилизации углового движения летательного аппарата относительно центра масс. Принимаем, что динамика системы стабилизации описывается линейными уравнениями в отклонениях относительно программного движения:

,

 ,                       

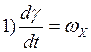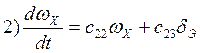, (3.1.1)

где:  - угол крена;  - угловая скорость крена;  - угол отклонения рулей элеронов;  - заданное значение угла крена;  и  - передаточные числа контура стабилизации крена; , - динамические коэффициенты, определяемые формулами:

,

,

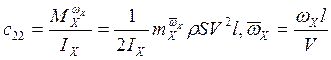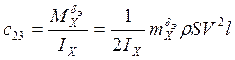где  - момент инерции ЛА относительно оси Х, - аэродинамические коэффициенты.

Первое и второе уравнения – уравнения объекта регулирования, третье – уравнение системы управления. В уравнениях 1,2,3 (3.1.1) пренебрегают инерционностью рулевой машины и запаздыванием в рулевом тракте.

Передаточная функция ЛА, характеризующая передачу воздействия от входа до выхода , имеет вид:

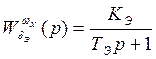,     (3.1.2)

где 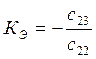   - коэффициент усиления ЛА,  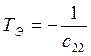- постоянная времени ЛА, характеризующая быстроту протекания переходного процесса. Численные значения коэффициентов приведены в таблице 3.1.1.

Таблица 3.1.1:

-3	22	0.8	1,2

Структурная схема контура стабилизации угла крена беспилотного ЛА представлена на рис. 3.1.1.

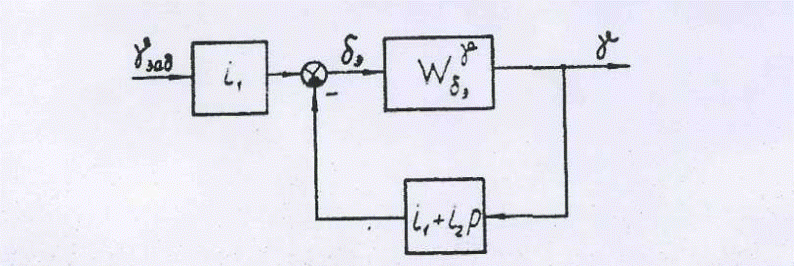
Рис. 3.1.1. Структурная схема контура стабилизации угла крена беспилотного ЛА.

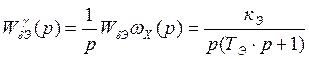
3.2 Исследование характеристик инерционного и колебательного звеньев аналитически и моделированием (определение весовой и переходной функции, частотных характеристик).

Определение частотных характеристик инерционного и колебательного звеньев.

А. Инерционное звено.

Передаточная функция инерционного звена в теории автоматического управления записывается в ви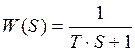де:

, где .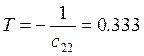

Для определения частотной характеристики звена подставим  . Тогда получим:

;

;

;

.

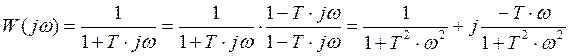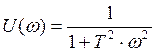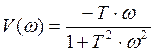Отсюда находим амплитудную и фазовую частотные характеристики:

;

,

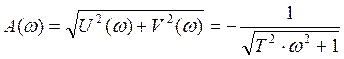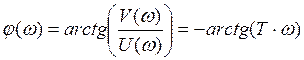и его логарифмическую амплитудную частотную характеристики:

;

.

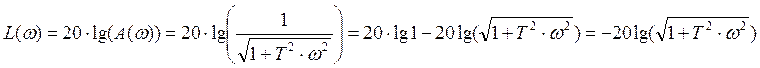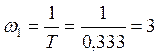 -частота сопряжения.

В. Колебательное звено.

Передаточная функция этого звена в теории автоматического управления записывается в ви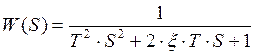де:     , где

- постоянная времени колебательного звена; - коэффициент демпфирования.

Для определения частотной характеристики звена запишем . 

;

;

;

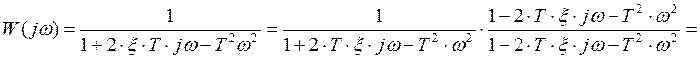
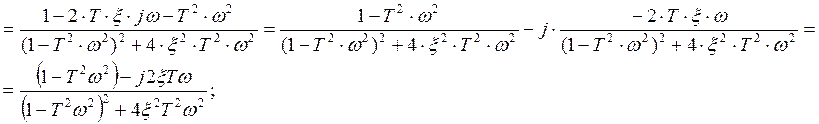
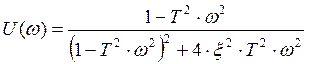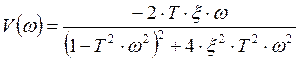Отсюда находим амплитудную и фазовую частотные характеристики звена:

;

;

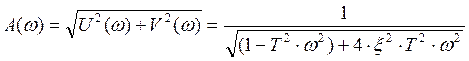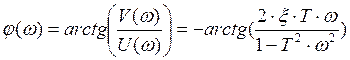и логарифмическую амплитудную характеристику:

.

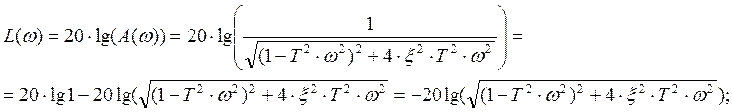
ЛАХ и асимптотическая ЛАХ  инерционного и колебательного звеньев представлены на рис. 3.2.2: