

















Министерство образования и науки Российской Федерации
Балтийский государственный технический университет «Военмех»
Кафедра Процессов управления
Петрова И.Л., Пономарев А.Н.
ИССЛЕДОВАНИЕ ДИНАМИКИ ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ.
Лабораторный практикум.
Санкт-Петербург
2008
ИССЛЕДОВАНИЕ ДИНАМИКИ ЛИНЕЙНОЙ САУ.
Лабораторная работа №1.
Определение динамических и частотных характеристик линейных систем автоматического управления методом моделирования.
Цель: Изучение методов определения весовых функций и частотных характеристик системы автоматического управления (САУ).
Описание работы и исходные данные:
Рассмотрим систему стабилизации углового движения ЛА относительно ц.м. в продольной плоскости. В качестве программного движения принимается полет ЛА на заданной высоте с постоянной скоростью. Принимается, что динамика системы стабилизации описывается линейными дифференциальными уравнениями в отклонениях относительно программного движения:
1) 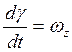 ;
;
2) 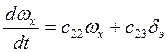 ; (1)
; (1)
3) ![]() ,
,
где ![]() -
угол крена;
-
угол крена; ![]() - угловая скорость крена;
- угловая скорость крена; ![]() - угол отклонения рулей элеронов;
- угол отклонения рулей элеронов; ![]() - заданное значение угла крена;
- заданное значение угла крена; ![]() ,
,![]() -
передаточные числа контура стабилизации крена. В системе уравнений (1)
индекс
-
передаточные числа контура стабилизации крена. В системе уравнений (1)
индекс ![]() (отклонение от программных значений)
опущен.
(отклонение от программных значений)
опущен.
Передаточная функция ЛА, характеризующая передачу
воздействия от входа ![]() , до выхода
, до выхода![]() , имеет вид
, имеет вид
|
(2) |
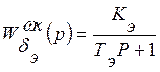
где 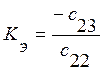 -
коэффициент усиления ЛА;
-
коэффициент усиления ЛА; 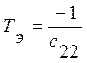 - постоянная
времени ЛА.
- постоянная
времени ЛА.
|
|||||||||||||||||||
 |
|||||||||||||||||||
|
|
||||||||||||||||||
|
|||||||||||||||||||
|
|
||||||||||||||||||
 |
 |
||||||||||||||||||



![]()
![]() - -
- -
|
|||||||

Рис.1.
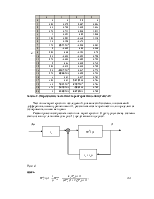
Численные значения коэффициентов ![]() приведены
в табл.1. Значения коэффициентов
приведены
в табл.1. Значения коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() приведены в табл.2.
приведены в табл.2.
Задача 1. Определение весовых функций разомкнутой САУ.
Динамика углового движения неуправляемого ЛА описывается следующими дифференциальными уравнениями:
1)
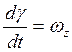 ;
;
2)
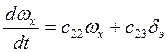 ; (3)
; (3)
Входным воздействием является
отклонение ![]() ; выходными
величинами -
; выходными
величинами - ![]() .
.
Весовой функцией или импульсной
переходной функцией динамической системы, имеющей один вход и один выход,
называется реакция системы в момент ![]() на единичный
импульс, действующий на систему в момент
на единичный
импульс, действующий на систему в момент ![]() .
.
Система (3) характеризуется весовыми функциями
![]() ;
; ![]() ,
,
которые определяются
моделированием, если на вход системы вместо ![]() подать
подать
![]() -функцию. Импульсная
-функцию. Импульсная ![]() -функция (дельта-функция Дирака)
определяется следующим образом:
-функция (дельта-функция Дирака)
определяется следующим образом:
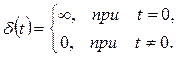 (4)
(4)
На основании
свойства ![]() -функции можно заменить воздействие в
виде
-функции можно заменить воздействие в
виде ![]() -функции начальными
условиями. Тогда весовые функции определяются моделированием однородной системы:
-функции начальными
условиями. Тогда весовые функции определяются моделированием однородной системы:
1) 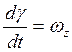 ;
;
2) 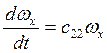 ;
(5)
;
(5)
c начальными условиями
![]() ;
; ![]() .
(6)
.
(6)
Таким образом,
для определения весовых функций ![]() ;
;
![]() , соответствующих
разомкнутой системе, необходимо выполнить моделирование системы (5) с
начальными условиями (6). Моделирование осуществляется на ЭВМ с использованием
программы, составленной в математическом пакете MathCad.
В этой программе система дифференциальных уравнений решается методом
Рунге-Кутта с постоянным шагом.
, соответствующих
разомкнутой системе, необходимо выполнить моделирование системы (5) с
начальными условиями (6). Моделирование осуществляется на ЭВМ с использованием
программы, составленной в математическом пакете MathCad.
В этой программе система дифференциальных уравнений решается методом
Рунге-Кутта с постоянным шагом.
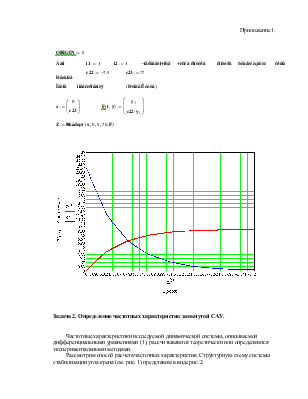
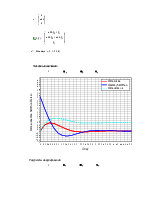
Решение поставленной задачи, полученное с использованием математического пакета MathCad, приведено в Приложении1:
Приложение1.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
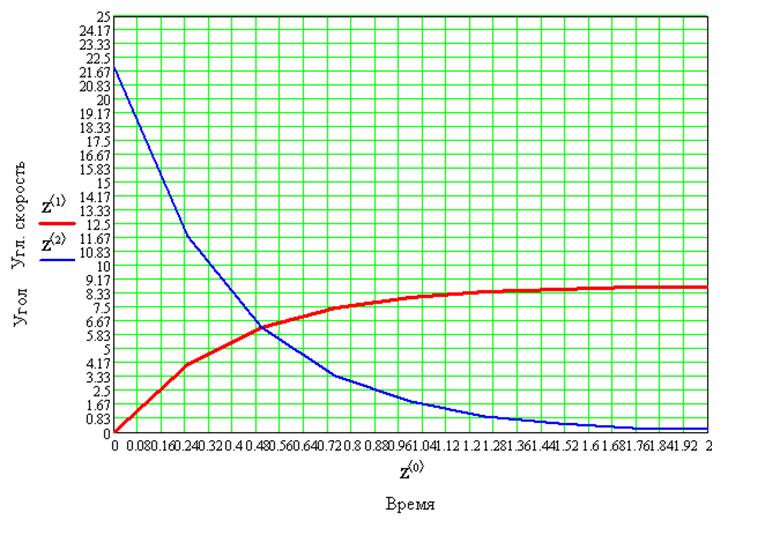
Задача 2. Определение частотных характеристик замкнутой САУ.
Частотные характеристики исследуемой динамической системы, описываемой дифференциальными уравнениями (1), рассчитываются теоретически или определяются экспериментальными методами.
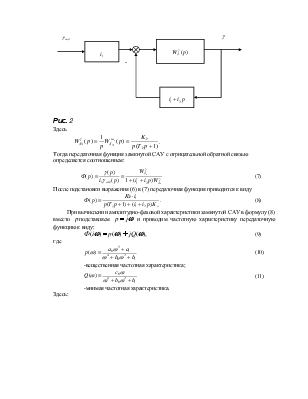
Рассмотрим способ расчета частотных характеристик. Структурную схему системы стабилизации угла крена (см. рис. 1) представим в виде рис.2.
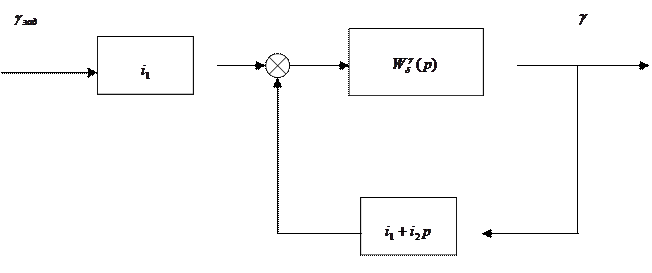 |
-
Здесь
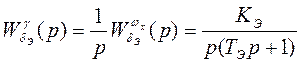 .
.
Тогда передаточная функция замкнутой САУ с отрицательной обратной связью определяется соотношением:
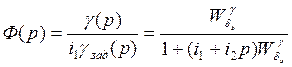 (7)
(7)
После подстановки выражения (6) в (7) передаточная функция приводится к виду
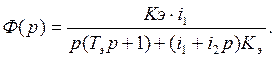 (8)
(8)
При вычислении амплитудно-фазовой характеристики замкнутой
САУ в формулу (8) вместо ![]() подставляем
подставляем ![]() и приводим частотную характеристику
передаточную функцию к виду:
и приводим частотную характеристику
передаточную функцию к виду:
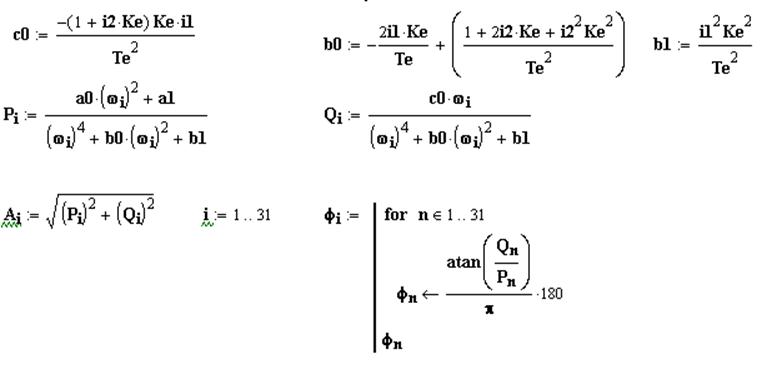
![]() (9)
(9)
где
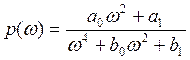 (10)
(10)
-вещественная частотная характеристика;
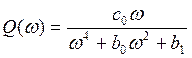 (11)
(11)
-мнимая частотная характеристика.
Здесь:
 (12)
(12)
Амплитудная и фазовая частотная характеристика замкнутой САУ определяются с помощью выражений :
![]() , (13)
, (13)
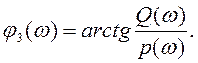 (14)
(14)
Для вычисления ![]() и
и ![]() используем
средства математического пакета MathCad.
используем
средства математического пакета MathCad.
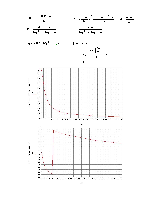
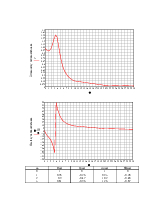
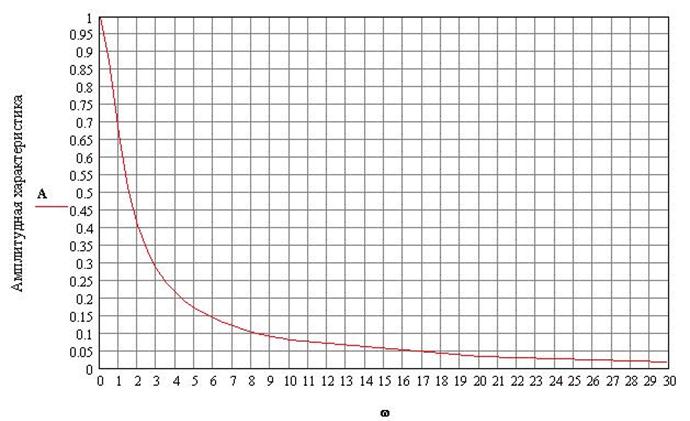
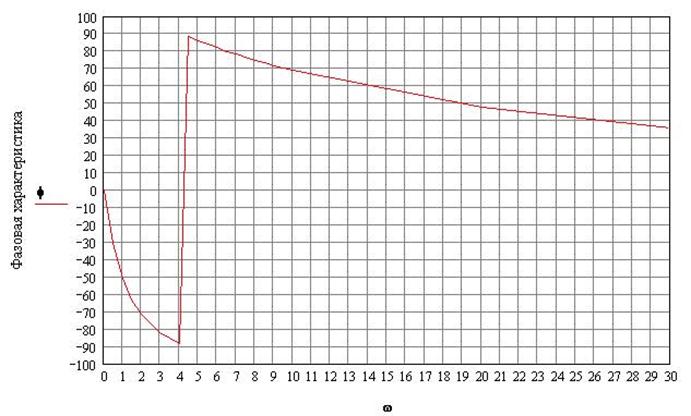
Результаты определения амплитудных и фазовых частотных характеристик теоретическим методом приведены в Приложении2.
Приложение2.

При исследовании реальных динамических систем на выход
системы подается гармоническое воздействие. В работе рассматривается
математическая модель (1). Для определения амплитуды ![]() моделированием
на ЭВМ воздействие
моделированием
на ЭВМ воздействие ![]() заменяется гармонической
функцией
заменяется гармонической
функцией ![]() Система дифференциальных уравнений
принимает следующий вид:
Система дифференциальных уравнений
принимает следующий вид:
1) 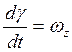 ;
;
2) 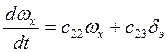 ;
;
3) ![]() , (15)
, (15)
![]()
Для решения системы (15) методом Рунге-Кутта используется программа составленная в математическом пакете MathCad. Программа решает систему дифференциальных уравнений (15) при десяти значениях частоты гармонических колебаний.
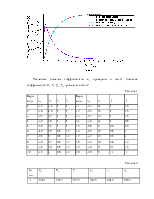
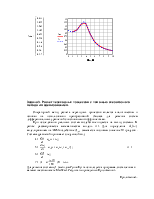
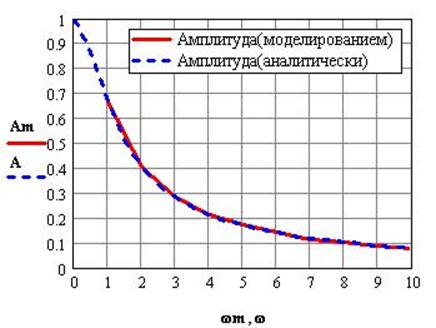
Результаты определения амплитудных и фазовых частотных характеристик экспериментальным методом приведены в Приложении3.
Приложение3.

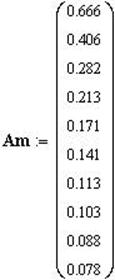
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.