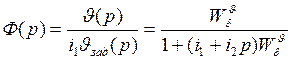Исследование динамики линейных систем управления беспилотных летательных аппаратов: Лабораторный практикум, страница 4

                                                     (7)

после подстановки выражения (6) в (7) передаточная функция приводится к виду

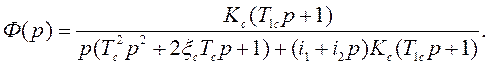                   (8)

При вычислении амплитудно-фазовой характеристики замкнутой САУ в формулу (8) вместо подставляем  и приводим частотную характеристику передаточную функцию к виду:

                                                               (9)

где

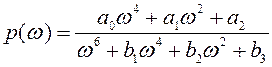                                                       (10)

-вещественная частотная характеристика;

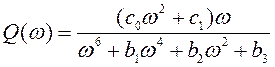                                                       (11)

-мнимая частотная характеристика.

здесь:

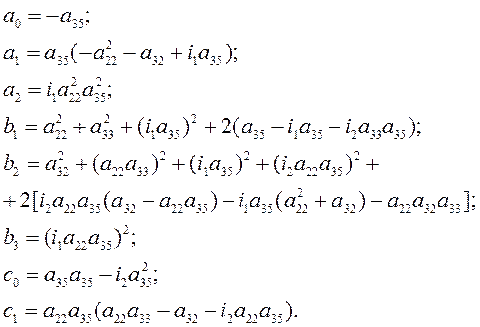                              (12)

Амплитудная и фазовая частотная характеристика замкнутой САУ определяются с помощью выражений :

,                                                               (13)

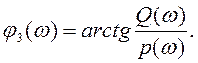                                                                 (14)

Для вычисления  и  используем средства математического пакета MathCad.

Результаты определения амплитудных и фазовых частотных характеристик теоретическим методом приведены в Приложении2.

Приложение2.

ω	P(ω)	Q(ω)	Aз(ω)	Φз(ω)
0 1 2 3 4 5 6 7 8 9 10 20 30 40 50 60 70 80 90 100 1000 ∞	1 0.95 0.9 0.81 -0.04 -0.52 -0.43 -0.31 -0.23 -0.18 -0.14 -0.03    -0.01 -8.05*10-3 -5.14*10-3 -3.57*10-3 -2.62*10-3 -2*10-3 -1.58*10-3 -1.28*10-3 -1.28*10-3 -1.28*10-3	0 -0.26 -0.47 -0.96 -1.31 -0.67 -0.3 -0.15 -0.09 -0.06 -0.04 -3.85*10-3 -1.1*10-3 -4.56*10—4 -2.32*10-4 -1.34*10-4 -8.41*10-5 -5.62*10-5 -3.95*10-5 -2.88*10-5 -2.87*10-8 -2.88*10-5 0	1 0.93 1.02 1.26 1.31 0.85 0.52 0.35 0.25 0.19 0.15 0.01 0.03 0.01 8.07**10-3 5.15*10-3 3.57*10-3 2.62*10-3 2*10-3 1.58*10-3 1.28*10--3 1.28*10-3 1.28*10-3	0 -0.28 -0.48 -0.87 1.54 0.91 0.61 0.45 0.36 0.31 0.26 0.12 0.08 0.06 0.05 0.04 0.03 0.03 0.02 0.02 2.24*10-3 0.02

При исследовании реальных систем гармоническое воздействие подается на выход системы. В работе рассматривается математическая модель (1). Для определения  моделированием на ЭВМ воздействие  заменяется гармонической функцией  Система уравнений принимает следующий вид:

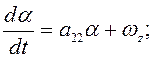
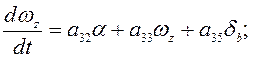
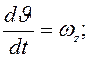                                                                                               (15)

Для решения системы (15) методом Рунге-Кутта используется программа, составленная в математическом пакете MathCad. Программа решает систему уравнений (15) при десяти значениях частоты гармонических колебаний.

Результаты определения амплитудных и фазовых частотных характеристик экспериментальным методом приведены в Приложении3.

Приложение3.

Задача 3. Расчет переходных процессов с помощью операторного метода и моделированием.

Операторный метод расчета переходных процессов является аналитическим и основан на использовании преобразований Лапласа для решения систем дифференциальных уравнений с постоянными коэффициентами.

При исследовании реальных систем воздействие подается на выход системы. В работе рассматривается математическая модель (1). Для определения  моделированием на ЭВМ воздействие  заменяется числовым значение 10 градусов . Система уравнений принимает следующий вид:

4)  ;

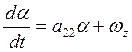5) 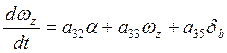 ;                                                                (1^*)

6)  ;

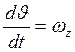7)  ,

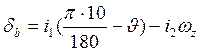Для решения системы (1^*) методом Рунге-Кутта используется программа, составленная в математическом пакете MathCad. Результаты приведены в Приложении4.

Приложение4.

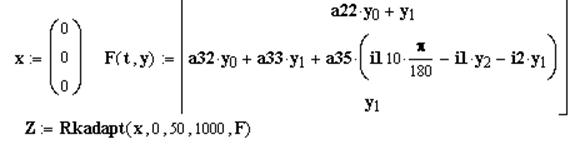
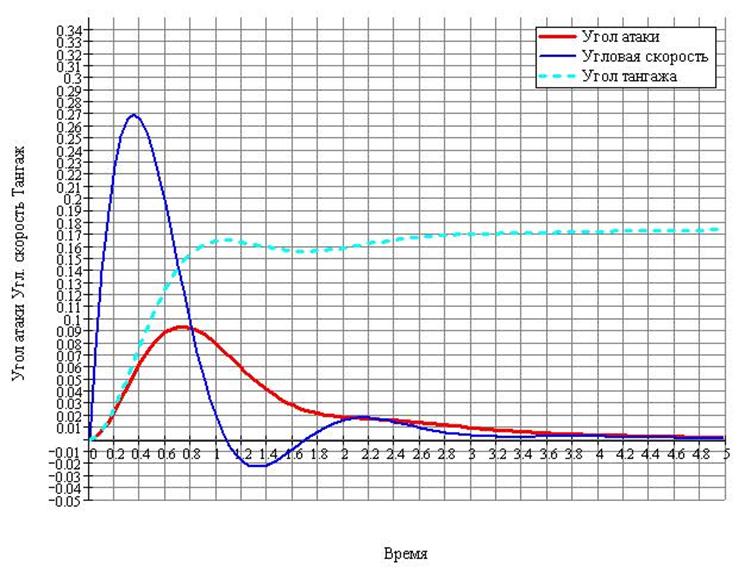
Переходные процессы, рассчитанные с помощью операторного метода и моделированием, строятся на одном графике и сравниваются:

Численные значения коэффициентов  приведены в табл.1. Значения коэффициентов , , ,  приведены в табл.2.

Таблица  1