Исследование динамики линейных систем управления беспилотных летательных аппаратов: Лабораторный практикум, страница 2

Задача 3.

Расчет переходных процессов с помощью операторного метода и моделированием.

Операторный метод расчета переходных процессов является аналитическим и основан на использовании преобразований Лапласа для решения систем дифференциальных уравнений с постоянными коэффициентами.

Рассмотрим процесс построения переходного процесса в системе дифференциальных уравнений (1) при стабилизации заданного значения угла крена  c нулевым начальными условиями:

; ; ;                                                                         (16)

;  ;  ;   .

Величину  можно принять как .

Применим преобразование Лапласа к системе уравнений (1), сохраняя для изображений те же обозначения, что и для оригиналов, однако, рассматривая их как функции переменной . Получим

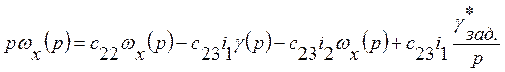           (17)

или

;          (18)

В (2.4)  - изображение по Лапласу входного воздействия. Определитель системы (5) равен:

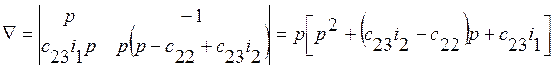.                     (19)

Используя правило Крамера, найдем изображение по Лапласу функции :

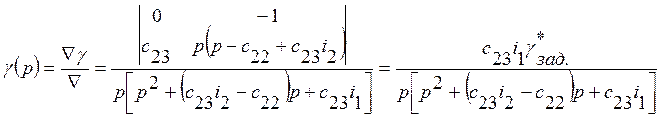.        (20)

Аналогично находится изображение по Лапласу функции :

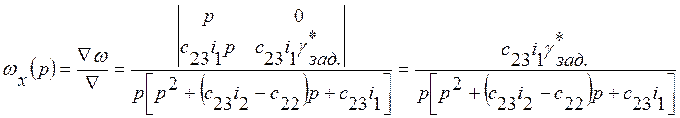.     (21)

Для нахождения оригинала функций  и  вычислим корни характеристического уравнения системы (1):

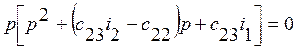.                                                                        (22)

из него находим

;  

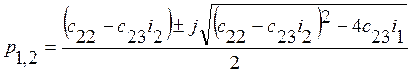
Если второй и третий корни представляют собой пару комплексно-сопряженных корней, т.е. , где

;

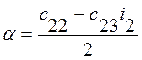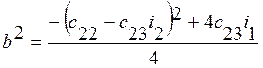
то левую часть характеристического уравнения можно записать в виде

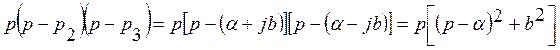
в этом случае

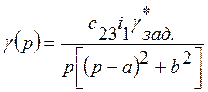.                                                                                          (23)

Из таблиц изображений функций по Лапласу выбираем формулу, соответствующую выражению (22):

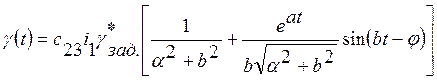,                                            (24)

где . Аналогично определяем 

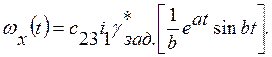                                                                              (25)

Если корни  и  является вещественными (, ),

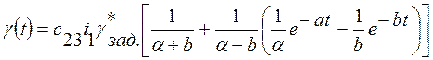.                                             (26)

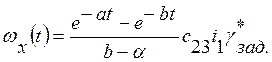                                                                              (27)

Расчет произведен в математическом пакете MathCad. Результаты решения приведены в Приложении4.

Приложение 4.

Дано:

Решение:

т.к. p2,p3 – это не комплексные корни, то функции  и :

При исследовании реальных систем воздействие подается на выход системы. В работе рассматривается математическая модель (1). Для определения  моделированием на ЭВМ воздействие  заменяется числовым значение 10 град. Система дифференциальных уравнений принимает следующий вид:

1)  ;

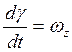2)  ;

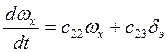3)  ,                                                                                      (28)

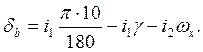
Для решения системы уравнений (28) методом Рунге-Кутта используется программа, составленная в математическом пакете MathCad. Результаты решения приведены в Приложении 5.

Приложение5.

Переходные процессы, рассчитанные с помощью операторного метода и моделированием, строятся на одном графике и сравниваются:

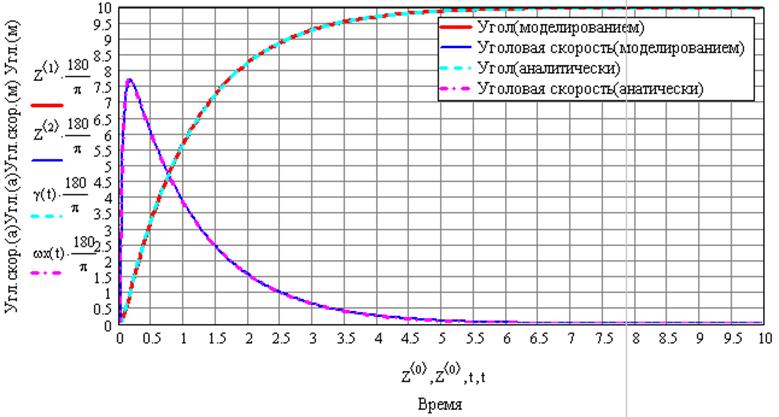
Численные значения коэффициентов  приведены в табл.1. Значения коэффициентов , , ,  приведены в табл.2.

Таблица 1

Вари­анты					Вари­анты
I	-1,9	3,9	I	I	11	-2,3	14	I	1,5
2	-1,8	4,0	I	I	12	-2,5	15	I	1,5
3	-2,5	22	I	I	13	-2,7	12	I	1,5
4	-3,0	18	I	I	14	-3,0	14	I	0,8
5	-5,0	25	I	I	15	-0,8	6	0,6	0,9
6	-4,0	20	0,8	1,2	16	-5,0	22	0,8	1
7	-0,5	5	0,8	1,2	17	-3,2	19	0,5	1
8	-3,0	22	0,8	1,2	18	-3,5	20	0,8	1,2
9	-3,0	20	0,8	1,2	19	-3,0	21	0,7	1,5
10	-1,5	4	0,8	1,2	20	-2,0	5	1,1	1

Таблица 2

№ п/п
1	0.701	2.677	0.179	0.476	0.042	0.592
2	0.534	2.414	0.147	0.386	0.048	0.994
3	1.040	0.669	0.169	0.163	0.085	1.469
4	0.012	3.187	0.227	0.304	0.051	0.466
5	0.870	4.100	0.204	0.333	0.045	0.502
6	1.325	1.245	0.217	0.280	0.055	0.558
7	1.354	3.977	0.447	0.507	0.063	0.131
8	0.862	0.839	0.091	0.148	0.060	3.625
9	0.658	1.526	0.129	0.369	0.042	1.177
10	0.845	1.092	0.111	0.161	0.058	2.340