Заметим, что можно составлять уравнения и по-другому, например, для левой части, если сила слева. Линия влияния получится такой же, но расчет будет сложнее.
Для консольных сечений всегда рассматривают равновесие отсеченной консоли. В этом случае в уравнения равновесия консоли входит не более двух усилий – либо Q (или М) и Р = 1, либо одна Q(или М).
58. Порядок построения линий влияния при узловой передаче нагрузки
1) Строится линия влияния искомого усилия обычным образом, т. е. без учета узловой передачи нагрузки; 2) выделяются ординаты этой линии влияния под узлами; 3) узловые ординаты соединяются прямыми линиями.
59. Определение усилий по линиям влияния от одной сосредоточенной силы Р
Если на систему действует одна вертикальная сила, то для определения значения S от этой силы необходимо ординату линии влияния S, измеренную под силой, умножить на величину Р:
S = Py,
где S – искомое усилие, y – ордината л. в. S под сечением, в котором расположена сила Р.
Ординаты берутся со своими знаками. Если внешняя сила направлена вертикально вверх (противоположно грузу Р = 1), то ее значение при умножении на соответствующую ординату линии влияния принимается отрицательным.
60. Определение усилий по линиям влияния от n сосредоточенных сил
Когда на балку действует n сосредоточенных вертикальных сил, следует найти ординаты л. в. S под этими силами, умножить каждую из них на соответствующую силу и на основании принципа суперпозиции полученные произведения просуммировать:
, где S – искомое усилие, yi – ордината л. в. S под i-м сечением балки, в котором
расположена сила Рi.
61. Определение усилий по линиям влияния от нагрузки, распределенной по некоторому закону q(z)
Пусть на некотором участке балки a–b приложена распределенная нагрузка интенсивностью q(z). Величина искомого усилия S
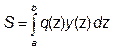, где y(z) – уравнение линии влияния S.
62. Определение усилий по линиям влияния от равномерно распределенной нагрузки
Если на балку действует равномерно распределенная нагрузка (q = const), то искомое усилие
, где ω – площадь линии влияния на участке действия нагрузки q.
Если равномерно распределенная нагрузка располагается над линией влияния, имеющей m участков, то формула для определения усилия S имеет вид
, где ωi – площадь i-го участка линии влияния, взятая с соответствующим знаком.
63. Как должна быть расположена равномерно распределенная нагрузка, чтобы ее положение для данного сечения являлось расчетным?
Строим линию влияния усилия S в данном сечении (это может быть М для балок, N для ферм и т. д.). Экстремальное значение искомого усилия S получится при экстремальном значении площади w. Это будет в том случае, когда нагрузка расположится над всей площадью л. в. S одного знака. Максимальное и минимальное значения величины S можно подсчитать по формулам:
Smax = qw(+); Smin = qw(–), где w(+), w(–) – площади соответственно положительной и отрицательной частей л. в. S под равномерно распределенной нагрузкой.
Если расчетное сопротивление растяжению и сжатию одинаково, то наибольшая по модулю величина будет расчетным значением усилия S
Sрасч = max (|Smin|, Smax ), а соответствующее ему положение нагрузки расчетным положением.
64. Как должна быть расположена сосредоточенная сила, чтобы ее положение для данного сечения являлось расчетным?
Строим линию влияния усилия S в данном сечении (это может быть М для балок, N для ферм и т. д.). Максимальное значение изучаемой величины Smax получается, если сила Р расположена над наибольшей ординатой ymax, минимальное Smin – над наименьшей ymin,
Smax = Рymax; Smin = Рymin,
Если расчетное сопротивление растяжению и сжатию одинаково, то наибольшая по модулю величина будет расчетным значением усилия S
Sрасч = max (|Smin|, Smax ), а соответствующее ему положение нагрузки расчетным положением.
65. Назовите основные типы балок
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.