РГР № 2. Расчет трёхшарнирной арки
Расчетная схема арки приведена на рисунке 1. Пролет l = 32 м,
стрела подъема f = 8 м, очертание оси – квадратная парабола ![]() , внешние нагрузки: q = 9 кН/м, P
= 60 кН; размеры поперечного сечения: высота h = 1 м, ширина b =
0,25 м; материал арки –
сосна; заданное сечение для построения линий влияния – 3.
, внешние нагрузки: q = 9 кН/м, P
= 60 кН; размеры поперечного сечения: высота h = 1 м, ширина b =
0,25 м; материал арки –
сосна; заданное сечение для построения линий влияния – 3.
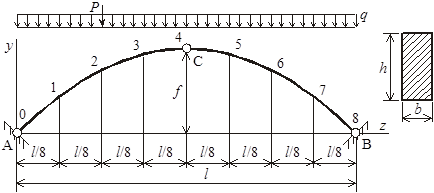
Рисунок 1
Положение k-го сечения (k = 0, …, 8) характеризуется тремя параметрами:
абсциссой ![]() , ординатой
, ординатой ![]() ,
углом между касательной к оси арки и осью z jk .
,
углом между касательной к оси арки и осью z jk .
Для вычисления jk продифференцируем функцию ![]() :
:
![]() . Отсюда
. Отсюда ![]()
Примечание.
Если очертание оси – синусоида, yk =
![]() ,
,
![]() , отсюда
, отсюда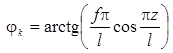 .
.
Принимая p = 3,142, расчеты необходимо вести в радианах, если же удобнее работать в градусах, то p = 180°.
Рассчитанные параметры арки записываем в таблицу 1.
Таблица 1. Геометрические параметры оси арки
|
№ сечения |
zk, м |
yk, м |
tg jk |
jk, рад |
sin jk |
cos jk |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 (A) |
0 |
0 |
1,00 |
0,785 |
0,707 |
0,707 |
|
1 |
4 |
3,5 |
0,75 |
0,644 |
0,600 |
0,800 |
|
2 |
8 |
6,0 |
0,50 |
0,464 |
0,447 |
0,894 |
|
3 |
12 |
7,5 |
0,25 |
0,245 |
0,243 |
0,970 |
|
4 (C) |
16 |
8,0 |
0 |
0 |
0 |
1 |
|
5 |
20 |
7,5 |
–0,25 |
–0,245 |
–0,243 |
0,970 |
|
6 |
24 |
6,0 |
–0,50 |
–0,464 |
–0,447 |
0,894 |
|
7 |
28 |
3,5 |
–0,75 |
–0,644 |
–0,600 |
0,800 |
|
8 (B) |
32 |
0 |
–1,00 |
–0,785 |
–0,707 |
0,707 |
Соответствующая рассматриваемой арке балка – это простая статически определимая балка, имеющая тот же пролет и схему нагружения (рисунок 2, а).
Опорные реакции балки VAб, VBб определяем из уравнений статики:
![]() ,
, ![]() ,
, ![]() ,
, ![]() , отсюда
, отсюда ![]() ,
,
![]() .
.
Проверка: ![]() ,
, ![]() .
.
Вычисляем внутренние поперечные силы Qkб и изгибающие моменты Мkб в k-ом сечении балки (k = 0, …, 8):
Q0б = VAб = 189 кН, М0б = 0;
Q1б = VAб – qz1 = 189 – 9 × 4 = 153 кН,
М1б = VAбz1 – qz12/2 = 189 × 4 – 9 × 42/2 = 684 кН × м;
Q2б лев = VAб – qz2 = 189 – 9 × 8 = 117 кН (левее силы Р),
Q2б прав = VAб – qz2 – Р = 189 – 9 × 8 – 60 = 57 кН (правее силы Р),
М2б = VAбz2 – qz22/2 = 189 × 8 – 9 × 82/2 = 1224 кН × м;
Q3б = – VВб + q(l – z3) = – 159 + 9 × 20 = 21 кН,
М3б = VBб(l – z3) – q(l – z3)2/2 = 159 × 20 – 9 × 202/2 = 1380 кН × м;
Q4б = – VВб + q(l – z4) = – 159 + 9 × 16 = – 15 кН,
М4б = VBб(l – z4) – q(l – z4)2/2 = 159 × 16 – 9 × 162/2 = 1392 кН × м;
Q5б = – VВб + q(l – z5) = – 159 + 9 × 12 = – 51 кН,
М5б = VBб(l – z5) – q(l – z5)2/2 = 159 × 12 – 9 × 122/2 = 1260 кН × м;
Q6б = – VВб + q(l – z6) = – 159 + 9 × 8 = – 87 кН,
М6б = VBб(l – z6) – q(l – z6)2/2 = 159 × 8 – 9 × 82/2 = 984 кН × м;
Q7б = – VВб + q(l – z7) = – 159 + 9 × 4 = – 123 кН,
М7б = VBб(l – z7) – q(l – z7)2/2 = 159 × 4 – 9 × 42/2 = 564 кН × м;
Q8б = – VВб = – 159 кН, М8б = 0.
Строим эпюры Qб, Мб в соответствующей балке (рисунок 2, б, в).
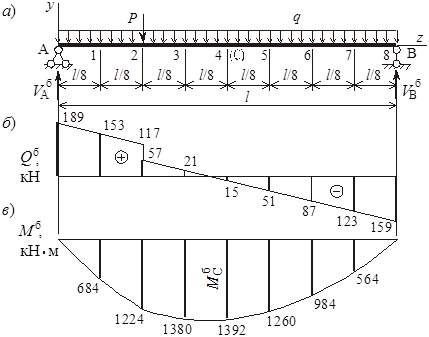
Рисунок 2
В опорах арки А и В возникают наклонные опорные реакции, которые можно разложить на четыре составляющие: вертикальные VA и VB, горизонтальные HA и HB (рисунок 3, а).
Вертикальные составляющие VA и VB равны опорным реакциям соответствующей балки
![]() ,
, ![]() .
.
Горизонтальные составляющие НA и НB равны между собой. Обозначим их Н (распор) и определим по формулам:
![]() ,
, ![]() , где МСб
– изгибающий момент в сечении С соответствующей балки.
, где МСб
– изгибающий момент в сечении С соответствующей балки.
Для рассматриваемой арки МСб = 1392 кН × м, Н = 1392/8 = 174 кН.
Внутренние усилия в k-ом сечении арки рассчитываем по формулам:
а) изгибающий момент ![]() ;
;
б) поперечная сила ![]() ;
;
в) продольная сила ![]() .
.
Расчет ведем в табличной форме (таблица 2). Величины zk, yk, sin jk, cos jk берем соответственно из граф 2, 3, 6, 7 таблицы 1, значения Mkб, Qkб – из эпюр M б, Q б.
Примечание. Так как в сечении 2 приложена сосредоточенная внешняя сила, эпюра Q б, а значит, и эпюры Q, N имеют в этом сечении скачок. Значения ординат внутренних усилий в графах 9, 10, 12, 13, 15, соответствующие точке левее сечения 2, приведены над чертой, точке правее сечения 2 – под чертой.
По полученным ординатам М, Q, N строим эпюры (рисунок 3, б, в, г).
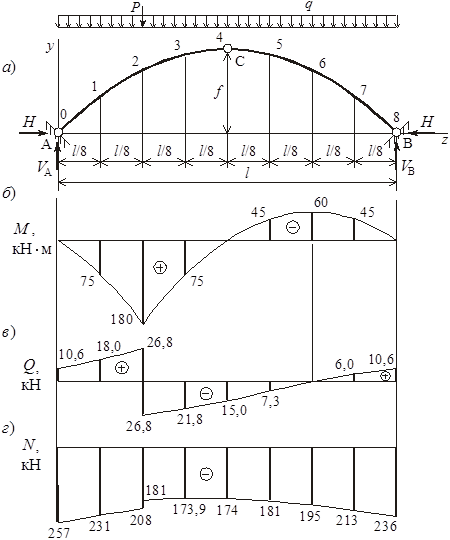
Рисунок 3
Таблица 2. Расчет внутренних усилий в арке
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.