Расчет трёхшарнирной арки (пролет - 32 м, стрела подъема - 8 м), страница 5

Вначале вычислим (из подобия треугольников) характерную ординату линии влияния N₃ , если груз Р = 1 расположен в сечении с абсциссой z = z₀^M :

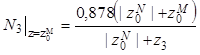 =  = 0,996.

Подсчитаем площади участков линий влияния.

w₁ = 0,5 z₀^M 1,875 = 0,5 · 14,2 · 1,875 = 13,31 м²;

w₂ = – 0,5 (l – z₀^M) 1,5 = – 0,5(32 – 14,2)1,5 = – 13,35 м²;

w₃ = – 0,5 z₃ 0,635 = – 0,5 · 12 · 0,635 = – 3,81 м;

w₄ = – 0,5 (z₀^M – z₃) (0,878 + 0,996) = – 0,5(14,2 – 12)1,874 = – 2,06 м;

w₅ = – 0,5 (l/2 – z₀^M) (1,092 + 0,996) = – 0,5(16 – 14,2)2,088 = – 1,88 м;

w₆ = – 0,5 (l/2) 1,092 = – 0,5 · 16 · 1,092 = – 8,74 м.

5.1 Положение I.

Определяем расчетное положение нагрузки по положительной части л. в. М₃ . Для этого располагаем распределенную нагрузку над участком  л. в. М₃, имеющим знак «+», а сосредоточенную силу – над максимальной ординатой этого участка. Находим +М_3max, умножая интенсивность распределенной нагрузки q на площадь линии влияния М₃, находящуюся под этой нагрузкой, а величину сосредоточенной силы P  – на ординату л. в. под силой.

Наибольший положительный момент

+М_3max = qω₁ + P ∙ 1,875 = 9 ∙ 13,31 + 60 ∙ 1,875 = 232,5 кН ∙ м.

Соответствующее +М_3max значение продольной силы N₃ :

N₃(+М_3max) = q(ω₃ + ω₄) + P ∙ (–0,878) =  9 (–3,81 – 2,06) – 60 ∙ 0,878 =

= –105,7 кН.

Нормальные напряжения в верхних волокнах

σ_в (+М_3max) =  =

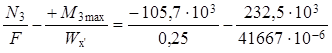= ( – 0,42 – 5,58) × 10⁶ = – 6,00 × 10⁶ Па = – 6,00 МПа.

Нормальные напряжения в нижних волокнах

σ_н (+М_3max) =  =

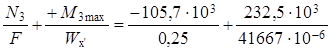= ( – 0,42 + 5,58) × 10⁶ =  5,16 × 10⁶ Па = – 5,16 МПа.

5.2 Положение II.

Определяем расчетное положение нагрузки по отрицательной части л. в. М₃. Для этого располагаем распределенную нагрузку над участком  л. в. М₃, имеющим знак «–», а сосредоточенную силу – над максимальной ординатой этого участка. Находим –М_3max и соответствующее ему значение продольной силы N₃.

Наибольший отрицательный момент

–М_3max = qω₂ + P ∙ (–1,5) = 9 (–13,35) – 60 ∙ 1,5 = –210,0 кН ∙ м.

Соответствующее +М_3max значение продольной силы N₃ :

N₃(–М_3max) = q(ω₅ + ω₆) + P ∙ (–1,092) = 9 (–1,88 – 8,74) – 60 ∙ 1,092 =

= –160,8 кН.

Нормальные напряжения в верхних волокнах

σ_в (–М_3max) =  =

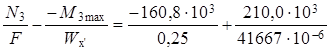= ( – 0,64 + 5,04) × 10⁶ = 4,40 × 10⁶ Па = 4,40 МПа.

Нормальные напряжения в нижних волокнах

σ_н (–М_3max) =  =

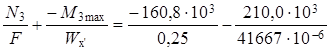= ( – 0,64 – 5,04) × 10⁶ = – 5,68 × 10⁶ Па = – 5,68 МПа.

5.3 Положение III.

Определяем расчетное положение нагрузки по л. в. N₃. Для этого располагаем распределенную нагрузку над всей л. в. N₃, так как вся она имеет знак «+», а сосредоточенную силу – над максимальной ординатой л. в.  Находим N_3max и соответствующее ему значение момента М₃ при данном положении нагрузки.

Наибольшая продольная сила

N_3max = q (ω₃ + ω₄ + ω₅ + ω₆) + P ∙ (–1,092) = 9 ( – 3,81 – 2,06 – 1,88 – 8,74) –

– 60 ∙ 1,092  =  –213,9 кН.

Соответствующее N_3max значение момента M₃ :

М₃(N_3max) = q (ω₁ + ω₂) + P ∙ (–1,5) = 9 (13,31 – 13,35) – 60 ∙ 1,5  = –90,1 кН ∙ м.

Нормальные напряжения в верхних волокнах

σ_в (N_3max) =  =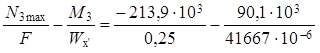

= ( – 0,85 – 2,16) × 10⁶ = –3,01 × 10⁶ Па = –3,01 МПа.

Нормальные напряжения в нижних волокнах

σ_н (N_3max) =  =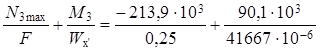

= ( – 0,85 + 2,16) × 10⁶ = 1,31 × 10⁶ Па = 1,31 МПа.

Наибольшие положительные напряжения  6,00 МПа  возникают при положении I внешней нагрузки, наибольшие отрицательные напряжения –5,68 МПа – при положении II.  Так как материал арки (сосна) одинаково хорошо сопротивляется и растяжению, и сжатию, наиболее опасными являются максимальные по модулю (в данном случае положительные) напряжения  6 МПа.

Следовательно, невыгоднейшим является нагружение, соответствующее  положению I  внешней нагрузки.