Расчет трёхшарнирной арки (пролет - 32 м, стрела подъема - 8 м), страница 4

По полученным ординатам в одном масштабе по одну сторону от базы строим линии влияния Q₃^б cos j₃ и (–Н × sin j₃) (рисунок 7, б, в). Совмещаем их  на  одной  базе  и  суммируем  соответствующие  ординаты (рисунок 7, г).

Характерные ординаты линии влияния Q₃ определяем из подобия треугольников. Изображаем л. в. Q₃ на горизонтальной базе (рисунок 7, д). Прямая,  соединяющая  ординаты  л. в. Q₃  левее сечения 3, называется левой прямой;   правее сечения 3, но левее шарнира С – I правой прямой;   правее шарнира С – II правой прямой.

Для контроля построений рассчитаем абсциссу z₀^Q нулевой точки О_Q линии влияния Q₃ (когда груз Р = 1 находится на расстоянии z₀^Q от левой опоры, ).

 =  = 21,33 м.

Чтобы графически определить абсциссу нулевой точки, необходимо провести касательную к оси арки в рассматриваемом сечении. Параллельно ей нужно провести прямую через точку А до пересечения с прямой, соединяющей точки В и С. Абсцисса полученной точки О_Q будет равна z₀^Q (см. рисунок 7, а).

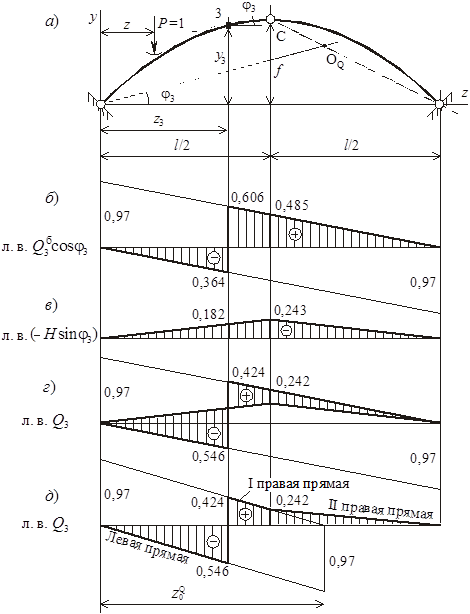
Рисунок 7

4.4 Линия влияния продольной силы

Для построения линии влияния  продольной  силы  N₃  в  сечении 3 арки (рисунок 8, а) используем формулу

.

Следовательно, чтобы получить л. в. N₃, необходимо построить линии влияния  Q₃^б× sin j₃  и  Н × cos j₃,  сложить их соответствующие ординаты и умножить на (–1).

Расчет ординат л. в. Q₃^б× sin j₃  и  л. в. Н × cos j₃ ведем в табличной форме (таблицы 8 и 9), используя данные таблиц 3 и 6.

Таблица 8. Расчеты для л. в. Q₃^б×sin j₃

Таблица 9. Расчеты для л. в. (–Н ×cos j₃)

По полученным ординатам в одном масштабе по разные стороны от базы строим линии влияния Q₃^б sin j₃ и Н × cos j₃ (рисунок 8, б, в). Совмещаем их на одной базе, суммируем соответствующие ординаты и умножаем на (–1) (рисунок 8, г).

Характерные ординаты линии влияния N₃ вычислим из подобия треугольников. Изображаем л. в. N₃ на горизонтальной базе (рисунок 8, д).  Прямая,  соединяющая  ординаты  л. в. N₃  левее сечения 3, называется левой прямой;   правее сечения 3, но левее шарнира С – I правой прямой;   правее шарнира С – II правой прямой.

Для контроля построений вычислим абсциссу z₀^N нулевой точки О_N линии влияния N₃ (когда груз Р = 1 находится на расстоянии z₀^N от левой опоры, ).

 =  = –4,57 м.

Чтобы графически определить абсциссу нулевой точки, необходимо провести касательную к оси арки в рассматриваемом сечении. Перпендикулярно ей нужно провести прямую через точку А до пересечения с прямой, соединяющей точки В и С. Абсцисса полученной точки О_N будет равна z₀^N (см. рисунок 8, а).

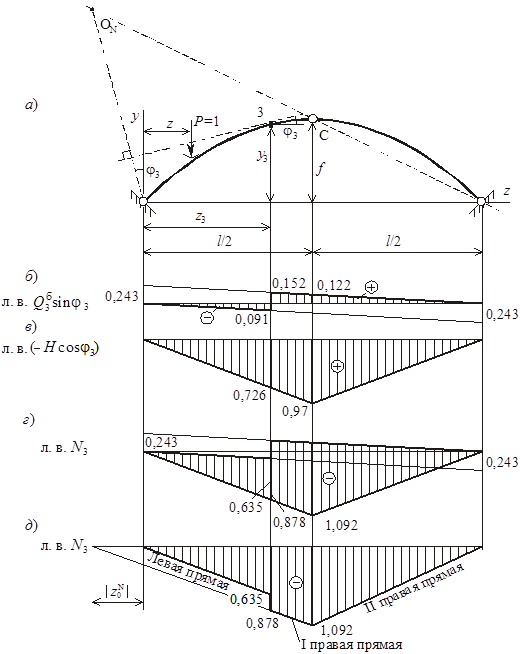
Рисунок 8

5 Определение невыгоднейшего нагружения

Предполагается, что арка нагружена сосредоточенной силой Р и равномерно распределенной нагрузкой q произвольной протяженности. Требуется определить такое положение нагрузки, при котором внутренние усилия в заданном сечении (сечение 3), а, следовательно, и нормальные напряжения будут наибольшими.

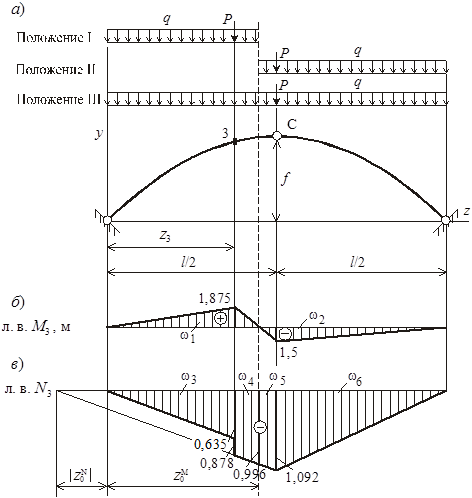
Рисунок 9

Арка работает на внецентренное сжатие, значит, на величину нормальных напряжений оказывают влияние значения продольных сил и изгибающих моментов (см. п. 4). Невыгоднейшее положение внешней нагрузки на сооружении определим приближенным методом, т. е. рассмотрим раздельно линии влияния N₃ и М₃. При этом рассмотрим три положения нагрузки на арке.