Расчет трёхшарнирной арки (пролет - 32 м, стрела подъема - 8 м), страница 3

4 Построение линий влияния усилий

Линии влияния строим в предположении, что по арке движется сосредоточенная сила (груз) Р = 1, направленная вертикально вниз. Ее положение  задается  координатой  z,  отсчитываемой  от  левой  опоры (рисунок 5, а).

4.1 Линии влияния опорных реакций

Вертикальные реакции V_A и V_B в арке равны реакциям V_A^б и V_B^б в соответствующей балке (рисунок 5, б), поэтому их линии влияния строим аналогично линиям влияния V_A^б и V_B^б (рисунок 5, в, г).

; ,  ;

;   ,  .

На опоре А  , ;  на опоре В  , .

Линию влияния распора Н построим статическим методом. Рассмотрим два положения подвижного груза (таблица 3).

Таблица 3. Расчеты для построения л. в. распора Н

Слева от шарнира С изображаем левую прямую, справа – правую. Их пересечение дает линию влияния Н (рисунок 5, д).

4.2 Линия влияния изгибающего момента

Для построения линии влияния изгибающего момента в заданном сечении арки (сечение 3) М₃ (рисунок 6, а) применяем способ наложения. При этом используем зависимость

М = М^б – Н × у.

То есть, чтобы получить л. в. М₃, необходимо построить линии влияния М₃^б и (–Н × у₃), а затем сложить их соответствующие ординаты.

Для расчета ординат л. в. М₃^б рассмотрим два положения груза Р = 1 на соответствующей балке (таблица 4).

Таблица 4. Расчеты для л. в. М₃^б

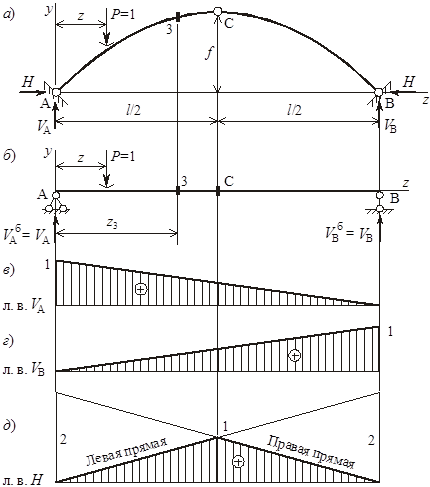
Рисунок 5

Для построения л. в. (Н × у₃) используем данные таблицы 3 и составляем таблицу 5.

Таблица 5. Расчеты для л. в. (–Н × у₃)

По полученным ординатам в одном масштабе по одну сторону от базы строим линии влияния М₃^б и (–Н × у₃) (рисунок 6, б, в). Далее совмещаем их  на  одной  базе  и  суммируем  соответствующие  ординаты (рисунок 6, г).

Характерные ординаты линии влияния М₃ вычисляем из подобия треугольников. По полученным ординатам изображаем л. в. М₃ на горизонтальной базе (рисунок 6, д). Прямая,  соединяющая  ординаты  л. в. M₃  левее сечения 3, называется левой прямой;   правее сечения 3, но левее шарнира С – I правой прямой;   правее шарнира С – II правой прямой.

Для контроля построений рассчитаем абсциссу z₀^М нулевой точки О_М линии влияния М₃ (когда груз Р = 1 находится на расстоянии z₀^М от левой опоры, ).

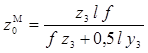 =  = 14,2 м.

Графически можно определить положение нулевой точки л. в. М₃ следующим образом. Необходимо соединить прямыми точки А и 3, а также точки В и С. Абсцисса точки пересечения полученных прямых О_М будет равна z₀^М (см. рисунок 6, а).

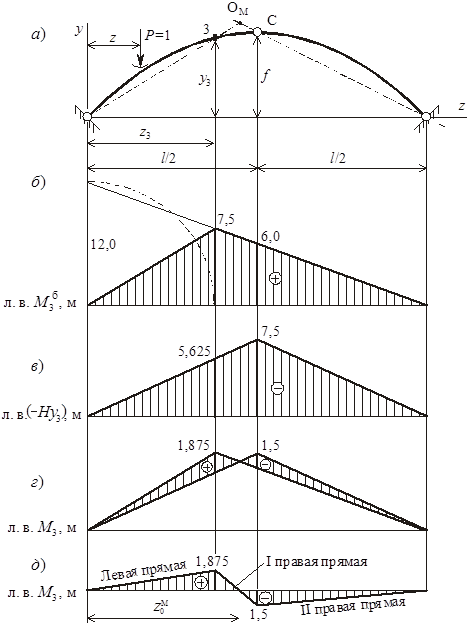
Рисунок 6

4.3 Линия влияния поперечной силы

Для построения линии влияния  поперечной  силы  Q₃  в  сечении 3 арки (рисунок 7, а) используем зависимость:

.

Следовательно, чтобы получить л. в. Q₃, необходимо построить линии влияния Q₃^б× cos j₃ и (–Н × sin j₃) и сложить их соответствующие ординаты.

Для расчета ординат л. в. Q₃^б  рассмотрим два положения груза Р = 1 на соответствующей балке (таблица 6).

Таблица 6. Расчеты для л. в. Q₃^б×cos j₃

Для построения л. в. (Н × sin j₃) используем данные таблицы 3 и составляем таблицу 7.

Таблица 7. Расчеты для л. в. (–Н ×sin j₃)