Расчет плоской рамы методом сил (внешние нагрузки: Р = 6 кН, q = 20 кН/м, длины стержней - 4 м)

Здесь С₂, С₃ – центры тяжести участков "первой" эпюры , Ω₂ = Ω₃ = l/2 – их площади,  ,  – ординаты "второй" эпюры , взятые под соответствующими центрами тяжести "первой".

Рисунок 8	Рисунок 9
Рисунок 10	Вычислим побочные единичные перемещения δ12 и δ21. Для этого перемножим эпюры  и  (рисунок 10).  = = . (Суммирования  нет,  так  как  эпюра   имеется  только  на  одном  участке). Здесь С1, Ω1 = l/2 – центр тяжести и площадь эпюры , – ордината , взятая под центром тяжести эпюры .

Грузовые перемещения подсчитаем по формуле частного случая перемножения эпюр, когда одна из них прямолинейна, а вторая ограничена квадратной параболой:

, где a, b, f – характерные ординаты параболы,  c, d, g – то же, прямолинейной эпюры.

Для определения перемещения Δ_1p  понадобятся эпюры  и , для Δ_2p  –  и  (рисунок 11, а, б).

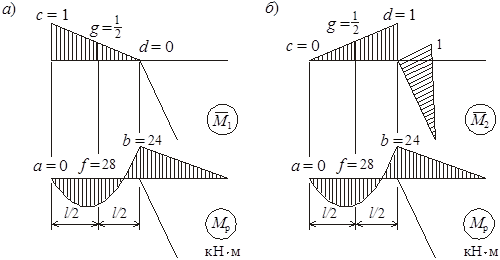
Рисунок 11

;

.

Заметим, что средние ординаты эпюр расположены по разные стороны от оси, поэтому их произведение отрицательно.

1.6 Проверка правильности вычисления перемещений

Строим суммарную единичную эпюру , складывая характерные ординаты эпюр  и :  =  +  (рисунок 12, а).  Находим условное суммарное единичное перемещение δ_SS, умножая  саму на себя:

Рисунок 12

=  = =  = . С другой стороны, δSS должно равняться сумме всех единичных перемещений δSS = δ11 + δ12 + δ21 + δ22 = = . Результаты совпали, значит, единичные перемещения вычислены верно.

Найдем условное суммарное грузовое перемещение Δ_sp, умножив эпюру  на M_p (рисунок 12, а, б):

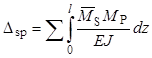 =  = , а также просуммировав грузовые перемещения

Δ_sp = Δ_1p + Δ_2p =  = .

Совпадение результатов говорит о правильности вычисления грузовых перемещений.

1.7 Решение системы канонических уравнений

Найденные значения единичных и грузовых перемещений подставляем в систему канонических уравнений (1):

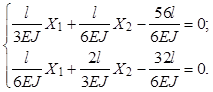                                    (2)

Умножим оба уравнения (2) на 6EJ/l и перенесем их свободные члены в правую часть. Получим:

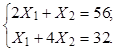                                            (3)

Решая систему, определяем неизвестные усилия X₁, X₂:

 кН ∙ м,    кН ∙ м.

Выполним проверку правильности вычисления X₁, X₂, подставив их значения в систему (3):

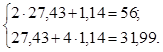
Точность подсчетов приемлема, погрешность составляет менее 1%.

1.8 Построение окончательной эпюры изгибающих моментов М

Вычислим ординаты окончательной эпюры изгибающих моментов М. Для этого необходимо сложить грузовую эпюру М_р и единичные , , умноженные на соответствующие значения X₁, X₂ (рисунок 13):

.

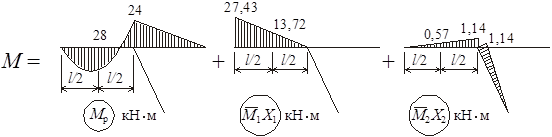
Рисунок 13

Подсчитаем значения изгибающего момента в характерных точках 1, …, 7 заданной системы (рисунок 14, а).

М⁽¹⁾ = 27,43 кН ∙ м, М⁽²⁾ = 24 + 1,14 = 25,14 кН ∙ м, М⁽³⁾ = 24 кН ∙ м,

М⁽⁴⁾ = 0 (растянуты верхние волокна);

М⁽⁵⁾ = 1,14 кН ∙ м, М⁽⁶⁾ = 0 (растянуты правые волокна);

М⁽⁷⁾ = 28 – 13,72 – 0,57 = 13,71 кН ∙ м (растянуты нижние волокна).

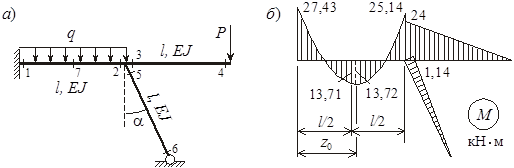
Рисунок 14

По полученным ординатам строим эпюру (рисунок 14, б). Экстремальное значение момента на участке 1–2 определим позже, после построения эпюры Q.

1.9 Проверка эпюры М

1.9.1 Статическая проверка

Рисунок 15

Для заданной расчетной схемы рамы статическая проверка  будет  состоять  в  вырезании  жесткого  узла 2–3–5 (рисунок 15)  и  выяснении  его  равновесия. Составим уравнение статики = 0; 24,15 – 24 – 1,14 = 0. Следовательно, узел находится в равновесии.

1.9.2 Деформационная проверка

Окончательная эпюра моментов М получена с использованием основной системы и может пониматься как эпюра в статически определимой системе при действии на нее заданной нагрузки и дополнительных усилий X₁, X₂.

Проверку лучше всего выполнять на другом варианте основной системы, так как эпюра М не зависит от выбранной о. с. Для деформационной проверки примем ее I-й вариант (см. рисунок 3, а).

Условное суммарное перемещение по направлениям неизвестных сил от совместного действия этих сил и внешней нагрузки должно равняться нулю:

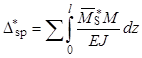 = 0.

Здесь  – суммарная единичная эпюра изгибающих моментов, построенная для I-го варианта основной системы. Для ее построения нагрузим раму одновременно двумя единичными усилиями ,  (рисунок 16, а) и рассчитаем значения момента  в характерных точках 1, …, 7 (k – номер точки).

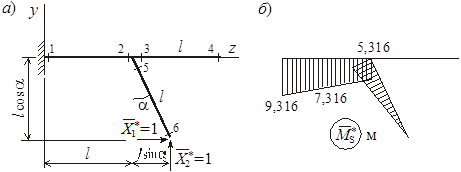
Рисунок 16

 =

= 4 ∙ 0,906 + 4(1 + 0,423) = 9,316 м;

=

= 4 ∙ 0,906 + 4 ∙ 0,423 = 5,316 м;

 =

= 4 ∙ 0,906 + 4(0,5 + 0,423) = 7,316 м (растянуты нижние волокна);

 = 5,316 м (растянуты левые волокна);

.

Условное суммарное перемещение подсчитаем по формуле частного случая перемножения эпюр, когда одна из них прямолинейна, а вторая ограничена квадратной параболой

 =  +

+  = .

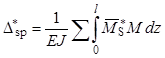Точность подсчетов приемлема. Равенство нулю величины  свидетельствует о том, что вертикальное и горизонтальное перемещения нижнего сечения рамы по направлениям приложенных единичных