Структурный анализ рычажного механизма. Кинематический анализ рычажного механизма. Кинематические диаграммы, страница 7

Для сложного движения (центра масс шатуна) обработку компьютерных данных в виде наглядных графических построений выполняют путем вычерчивания одного из годографов скорости или ускорения. В выбранных масштабах  или  длины отрезков на годографах определяют по формулам:

                       ; .                          (4.41)

Векторы  или  откладывают под углами соответственно  и . Их концы снабжают стрелками и номерами позиций и соединяют плавной кривой, которая и является годографом. Таким образом, годографом называется кривая, соединяющая  концы векторов, изображающих векторную величину.

В заданиях 02…04 ползуны диад второго вида имеют направляющие, расположенные вертикально либо наклонно. В этих случаях кинематику диады второго вида можно рассчитать по программе ТМ24 в системе QuickBASIC. Основной алгоритм соответствует рис. 4.3 и формулам (4.21)…(4.38). В диалоговом режиме студент выбирает схему: типовая ("да", если она соответствует рис. 4.3) или "нет".

В схемах, отличающихся от типовой, требуется ввести угол ψ между заданной схемой и типовой. Так, в механизмах трактора (рис. 2.2.1, а) направляющие обеих диад расположены под углом 90° по сравнению с типовой схемой (рис. 4.3). В этом случае угол между осями xи y  ψ = 90° автоматически прибавляется к задаваемому начальному углу φ₁ = 30° и к другим углам φ₁, вводимым по циклу с шагом Δφ₁ =30°. Так, для угла φ₁ = 90°, отсчитываемого от  положительного направления оси x, модули скоростей и ускорений будут соответствовать типовой схеме с φ₁ = 0°. Иначе говоря, при угле φ₁ = 0° ( положение кривошипа 3) рассчитываются параметры  по формуле типовой схемы, но в колонке "положения кривошипа" на распечатке ставится положение 12 или угол 90°. Направления линейных векторов и направляющий угол шатуна φ₂ также корректируется на угол ψ. Направления угловых скоростей ω₂ и ускорений ε₂ не изменятся в заданной схеме по сравнению с типовой.

В диаде ADE(рис. 2.2.1, а) кинематические параметры повторяются с интервалом 180° по сравнению с диадой ABC. В этом случае расчеты можно повторить, вводя угол между осями ψ = 90°+180° = 270° и получив новую распечатку. Более рационально использовать распечатку диады ABC, где колонку с номерами положений снабдить пометкой ABC, а рядом, на свободном поле распечатки создать колонку с пометкой ADE, где поместить номера положений, отличающихся на 6 в сравнении с первой колонкой ABC, например, против 1 ставить 7, против 2 ставить 8, против 10 - 4, против 12 - 6 и т. д.  (см. рис. 2.2.1, а). Пример откорректированной распечатки с исходными данными по заданию 01-13 приведен на рис. 4.5.

В механизме тепловозного дизеля (рис. 2.3.1, а) расчеты по программе ТМ24 можно выполнить только для диады ABC. Угол между осями xи y  определяют по формуле:

                                      ,                                                    (4.42)

где  - угол между осями цилиндров; при =60° 120°.

В механизме воздушного компрессора (рис. 2.4.1, а) углы между осями цилиндров и осью x определяют по формулам:

;

.

При  = 90° = 45°, = 135°.

В распечатках компьютерных данных углы векторов привязаны к оси x.

4.5.3. Кривошипно-коромысловый механизм

А) Аналитические выражения

Расчетная схема механизма  представлена на рис. 4.6. Длины звеньев заменены векторами , , , . Направляющие углы , ,  зависят от направления векторов и отсчитываются от положительного направления оси x против часовой стрелки при условии нахождения конца вектора в начале координат, так же как и другие векторы.

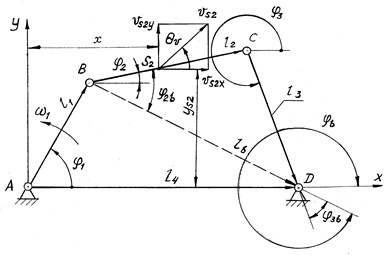
Рис. 4.6

Предварительно определяют коэффициенты длин звеньев:

; ; ; .                       (4.43)

.

Направляющие углы определяют по формулам:

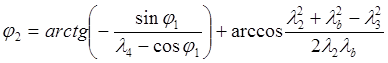                            .               (4.44)

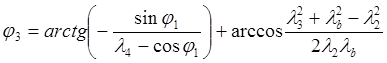                            .               (4.45)

Для приведения вторых слагаемых уравнений (4.44) и (4.45) к виду, удобному для ввода в ПЭВМ, используют выражение:

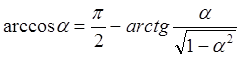                                          .                         (4.46)

Угловые скорости звеньев ω₂ и ω₃ определяют по формулам Крамера после дифференцирования уравнений проекций векторов, связанных со звеньями, на координатные оси.