Структурный анализ рычажного механизма. Кинематический анализ рычажного механизма. Кинематические диаграммы, страница 3

,                                                     (4.7)

где  - отрезок на плане скоростей, мм.

Так же определяется относительная скорость, вектор которой не проходит через полюс плана:

.

Направления искомых векторов определяют стрелки по уравнениям (4.4) либо по простому правилу: стрелки искомых векторов направляют в искомую точку.

Планы скоростей и ускорений обладают свойством подобия: каждой точке плана положений соответствует точка на плане скоростей и ускорений. По этому свойству из построенного плана скоростей  можно определить скорость любой точки механизма для заданного положения начального звена. Так, точка S₂ шатуна 2 на плане положений с линейной координатой l_BS2 имеет подобную точку S₂ на плане скоростей, которую находят из пропорции:

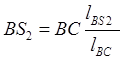.                                              (4.8)

Так, для точки S₂ шатуна механизма ДВС (рис. 4.1) при отношении l_BS2/l_BC=0,3bc, а вектор скорости  определяют соединением полюса p с точкой S₂. Модуль скорости центра тяжести шатуна

.

Модули искомых скоростей определяют по правилу: для определения физической величины длину отрезка на плане делят на масштаб, что реализовано в формуле (4.7). По данным из плана скоростей также определяют величину и направление угловой скорости. Для шатуна 2 модуль угловой скорости в с^-1:

.                                              (4.9)

Направление угловой скорости определяют, прикладывая вектор относительной скорости   в точку С шатуна (условно в соответствии с векторным уравнением (4.4) точка С вращается относительно точки В). В примерах на рис. 4.1 и 4.2  направление  отрицательное - по часовой стрелке. Ошибок при определении  и  можно избежать, изобразив расчётные схемы в виде шатунов, к вращающимся концам которых перпендикулярно им прикладывают векторы линейных скоростей и тангенциальных ускорений (рис. 4.1 и 4.2, г).

Для диады 4-5 рычажного механизма ДВС (рис. 4.1), где неизвестна кинематика точки Е, записывают вторую систему векторных уравнений:

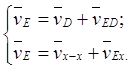.                                            (4.10)

Планы скоростей для обеих диад механизма ДВС строят на одном поле чертежа с общим полюсом p. В результате получают план скоростей механизма в целом (рис. 4.1), из которого можно определить скорость любой точки механизма. В соответствии с первым уравнением системы (4.10) из полюса p проводят вектор pd = - pb в сторону вращения точки D. Из его конца - направление   и т. д. в соответствии с векторными уравнениями. В искомую точку e приводят стрелки векторов, далее находят положение точки S₄ на отрезке de по свойству подобия, рассчитывают модули линейных скоростей  , ,  и угловой скорости .

Планы скоростей обеих диад имеют центральную симметрию, при этом =-, =-, а . Методика построения планов скоростей и ускорений диад первого и второго видов приведена в пособии [3].

4.3. План ускорений

Для искомой точки С диады 2-3 (рис. 4.2) записывают систему векторных уравнений:

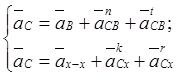,                                            (4.11)

где a_B - линейное постоянное ускорение точки B, м/с ²;  - относительное нормальное ускорение;  - относительное тангенциальное ускорение;  - кориолисово ускорение;  - относительное ускорение.

Линейное ускорение во вращательном движении раскладывают на нормальную и тангенциальную составляющие. Ускорение a_B имеет только нормальную составляющую, так как угловое ускорение = 0:

.                                            (4.12)

Нормальное ускорение направлено к центру вращения. Его определяют также по формуле:

.                                                (4.13)

Тангенциальное ускорение  является искомым, но имеет известное направление - перпендикулярно нормальному. Также известно направление относительного ускорения в поступательном движении  - вдоль направляющей. Кориолисово ускорение имеет место только в поступательной кинематической паре и только при вращающейся направляющей (задание 06). Модуль кориолисова ускорения

,                                                   (4.14)

где  - угловая  скорость направляющей;

 - относительная скорость в поступательной паре.