Математика \ Высшая математика

Вища математика: Навчальний посібник (англійською мовою), страница 7

The function is said to be decreasing if y decreases when the independent variable x increases:

2) The function is called the even one if the following equality holds:

.

The function is called the odd one if the following equality holds:

If the given function even or odd?

,      ,     

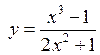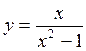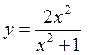
3) The periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions.

4. The basic elementary functions:

•  The power function;

•  The exponential function;

•  The logarithmic function;

•  The trigonometric functions ( 4 );

•  The inverse trigonometric functions ( 4 ).

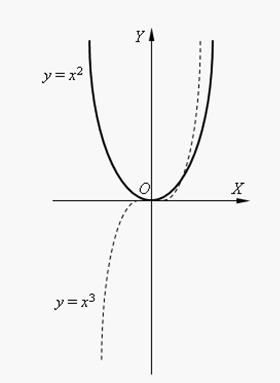
1) The power function:

Some particular cases:

а) : 

,   .

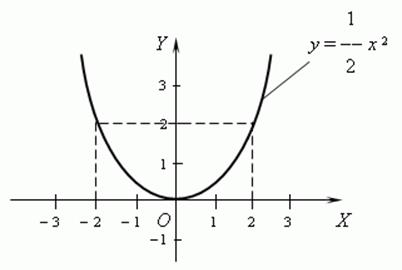
The properties of this function:

- even;

- decreasing on , increasing on ;

b) :  

,  .

The properties of this function:

- odd;

- increasing on  ;

c) : 

 


,   .

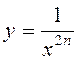
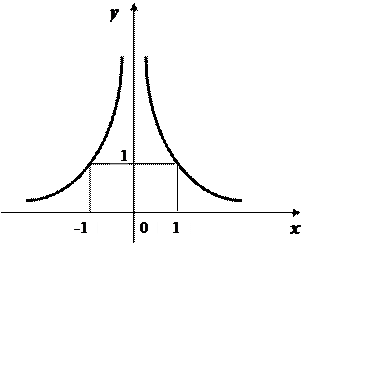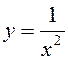
The properties of this function:

- even;

- increasing on (-∞; 0), decreasing on (0; +∞);

d) :  

 

,   .

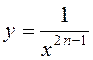
The properties of this function:

- odd;

- decreasing on  and .

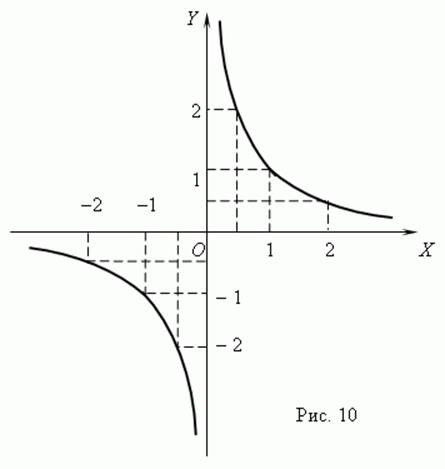
2) The exponential function: 

(a>1)
 

(0<a<1)
 

y=ax
 
 

   ,  .

If 0<a<1 then the function is decreasing, if a>1 then the function is increasing.

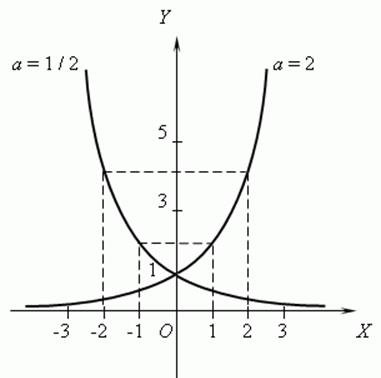
3) The logarithmic function:,  y=logax  (the log of x to the base of a)

 


,   .

If 0<a<1 then the function is decreasing, if a>1 then the function is increasing.

4) The trigonometric functions:

а)  

y=sinx
 

,  .

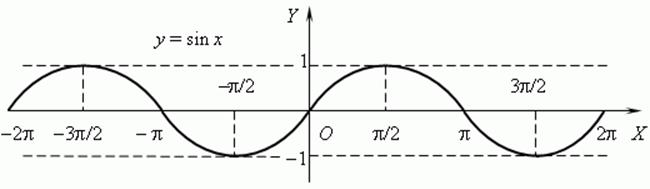
The function is odd and periodic,  periodT=2p.

The function is in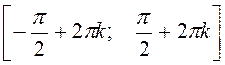creasing on , , the function is decreasing on , ;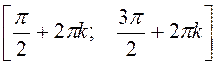

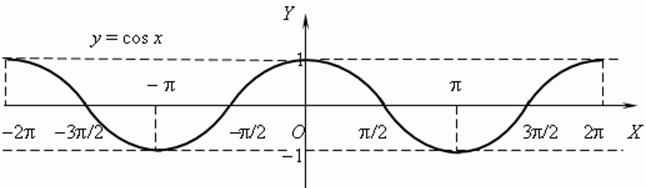
b) y=cosx,

 


,  .

The function is even and periodic,  periodT=2p.

The function is decreasing on , , the function is increasing on ,

c) y=tgx

,   .

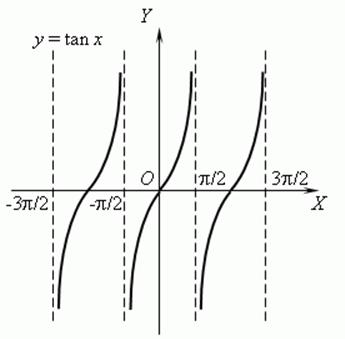
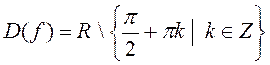The function is odd and periodic,  periodT=p.

The function is increasing on ;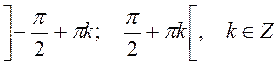

d) y=сtgx

,   .

Рис.9
 
The function is odd and periodic, periodT=p.

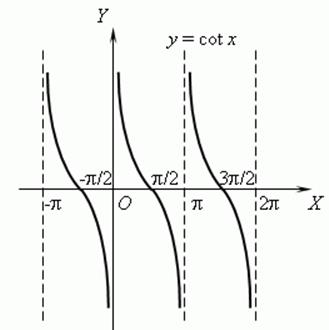
The function is decreasing on 

5) The inverse trigonometric functions:

а) y=arcsinx

,  .

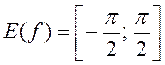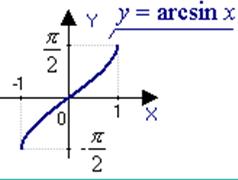
The function is odd and increasing.

b) y=arccosx

,  .

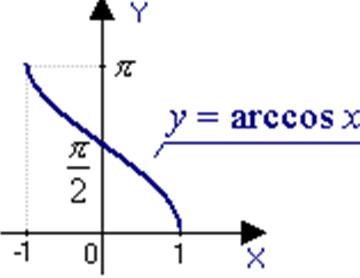
The function is decreasing.

c) y=arctgx,   ,  .

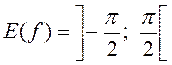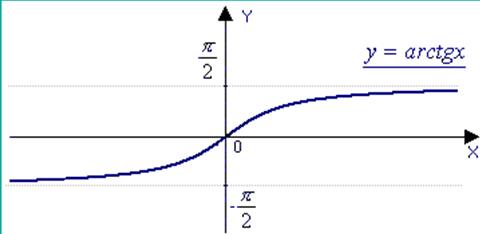
The function is odd and increasing.

d) y=arcсtgx,   ,  .

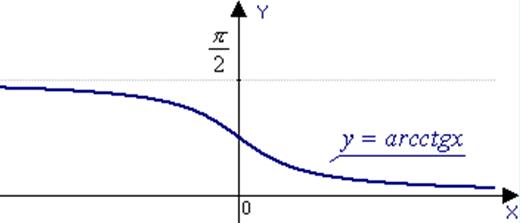
The function is decreasing.

4. y=f(u), u=g(x) → y=f(g(x)) – the composite function,

u – the intermediate variable, f(u) - external function, g(x) - internal function.

Examples.

5. An elementary function is a function of one variable built from a finite number of the basic elementary function and constants through composition and combinations using the four elementary operations (+ – × ÷).

Examples:

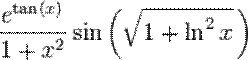\frac{e^{\tan(x)}}{1+x^2}\sin\left(\sqrt{1+\ln^2 x}\,\right),   , 

 

 



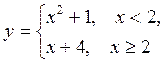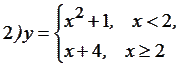Topic:Theory of limits

1.  Definition of the limit of function, the main properties of limits

2.  Infinitesimal magnitudes

3.  Infinitely large magnitudes

4.  The first remarkable limit and its corollaries

5.  The second remarkable limit and its corollaries

6.  The economic interpretation of the number e

1. Definition. A is a limit of f(x) as x approaches x0 if whenever x is infinitely close to x0 the value of function f(x) is infinitely close to A.

 


(There is more precise definition but we omit it)

x0 is the limit point, A is the limit value.

Examples:

 


It means that the value of f(x) gets close to 9 as x gets closer and closer to 3.

In most cases the function isn’t defined at the limit point x0. Pass to the next example:

 


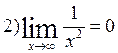This limit means that as x increases infinitely then function f(x) becomes infinitely close to 0.

In this case the function is called the infinitesimal magnitude or infinitesimal (as x approaches ∞).

Скачать файл