Assume that argument takes the value x=2. Then we can predict (forecast) that y=0,40·2+10,14=10,94.
Topic: Indefinite integral, its properties and methods of calculation
1. Definition and properties of indefinite integrals.
2. The table of indefinite integrals.
3. Integration by substitution.
4. Integration by parts.
5. Integration of the rational functions.
6. Integration of the trigonometric functions.
7. Integration of the irrational functions.
1. Definition. The function F(x) is called the antiderivative of the function f(x) on the interval (a, b), if at all points of this interval the equality F’(x)= f(x) holds.
Examples.
1) The antiderivative of the function f(x)=cosx is F(x)=sinx, since (sinx)’=cosx. What do you think are there other antiderivatives of this function? Besides, there are an infinite number of antiderivatives, which differ from each other by a constant: sinx+1, sinx+C, where C – an arbitrary constant. What do you think: could the function have absolutely different antiderivatives?
2) Let’s consider the inverse task: (Suppose wehave) The function F(x)=x3 is the antiderivative of the function f(x)=3x2, because (x3)’= 3x2. (whatis thisfunction?)
Let’s return to thequestion: How many antiderivatives may have the function?
The following theorem holds: If the function is continuous on some interval, it has infinite number of antiderivatives, which differ from each other by a constant.
Let’s pass to the main definition:
Definition. If the function F(x) is an
antiderivative of the function f(x), then the expression F(x)+C, where
C is an arbitrary constant, is called the indefinite integral of the
function f(x) and is denoted by the symbol
Thus, we have the following notation of the indefinite integral of the function f(x):
 |
where F’(x)= f(x), C - an arbitrary constant. Here the function f(x) is called the integrand; the differential dx indicates that x is the variable of integration.
So, we can say that the indefinite integral of a function is a set of all antiderivatives of this function.
The process of finding of the integral of the function is called integration of this function.
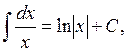
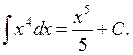Examples:
 |
The
main properties of the indefinite integrals
 |
||||
 |
||||
 |
||||
 |
||||
In particular, from this properties we can see, that integration is an inverse operation of differentiation (Without goingintodetails ...). The last two points are almost obviously, but they are very important for practice.
2. The table of the main indefinite integrals
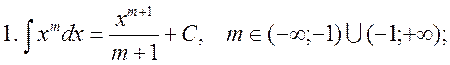
in particular,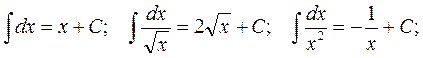 
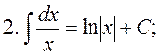
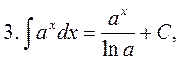in particular, 
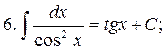
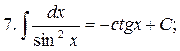
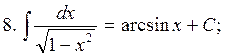
in the general case: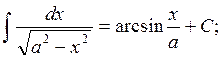 
in the general case: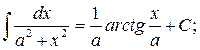 
 |
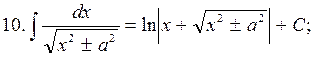
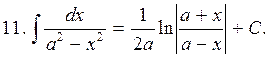
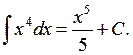To check this table it is sufficient to establish that the derivative of the right-hand side of each equality is equal to the integrand.
Most of the integrals are not tabulated. Usually, however, even in the simplest examples, the given integrals can not be found in the table. In this case we should transform the integral to one from the table. These transformations need some experience and practice.
We have to use theindividual approach to each integral, so, the operation of integration is more difficulty than the operation of differentiation. But on the otherhand there are somestandardtypes of integrals, which we are going to study.
3. Let’s consider the next special case of the integration by substitution, when the integrand has some special form: it contains a fixed function f(x) and also its derivative as a factor of the numerator. In this case we can use the following substitution: we put t = f(x), then dt=f’(x)dx. We should substitute these expressions in the given integral and, as a rule, we will get a tabular integral. Anyway it will be the simpler integral.
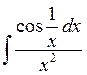
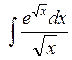Examples
, 
,
, 
,
,
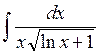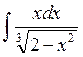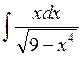Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.