One useful application of calculating the rank of a matrix is the computation of the number of solutions of a system of linear equations. According to the Kronecker–Capelli theorem, the system is inconsistent if the rank of the augmented matrix is greater than the rank of the coefficient matrix. If, on the other hand, ranks of these two matrices are equal, the system must have at least one solution. The solution is unique if and only if the rank equals the number of variables. Otherwise the general solution has k free parameters where k is the difference between the number of variables and the rank.
Kronecker–Capelli theorem is the theorem in linear algebra that allows to compute the number of solutions in a system of linear equations with the help of the ranks of its augmented matrix and coefficient matrix.
Theorem (Kronecker–Capelli). A system of linear equations with n variables has a solution if and only if the rank of its coefficient matrix is equal to the rank of its augmented matrix.
In particular:
1) if then the system is consistent, determined;
2) if then the system is consistent, underdetermined;
3) if then the system is inconsistent.
Examples:
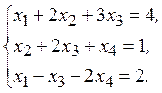
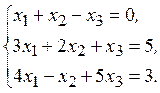 1) 2)
1) 2)
4. Homogeneous linear system is a system of the form:
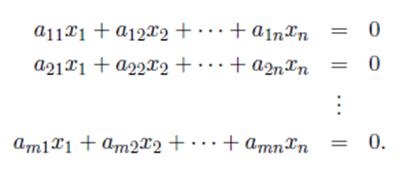
Such a system is always consistent as
![]()
is a solution. This solution is called the trivial solution. Any other solution is called a non-trivial solution.
Topic: Analytic geometry in the plane
1. The different types of equations of the straight lines in the plane.
2. The angle between the straight lines. The conditions of the parallelism and perpendicularity of two straight lines.
3. The distance from the point to the straight line.
4. The second-order curves.
1. Consider the different equations of the straight lines in the plane depending on the given conditions.
1.1.
![]()
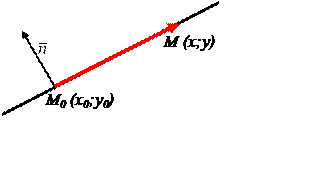
![]() - the normal vector,
- the normal vector,
![]() The
equation of the straight line, which
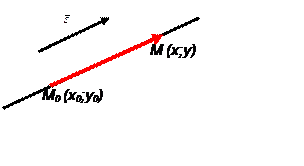
passes through the point M0(x0,y0)
and has the normal
vector :
The
equation of the straight line, which
passes through the point M0(x0,y0)
and has the normal
vector :
A(х-х0) + В(у-у0) =0(1)
1.2. Transform the
equation (1): Aх + Ву+ C
=0, ![]() - the normal
vector. This equation is called the common equation of the straight line in the plane. Consider some particular cases:
- the normal
vector. This equation is called the common equation of the straight line in the plane. Consider some particular cases:
1) B≠0: 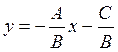 , in other notations y=kx+b, k
is a slope and b is intercept;
, in other notations y=kx+b, k
is a slope and b is intercept;
2) A=0, B≠0:
Ву+ C =0, 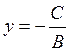 -the horizontal line;
-the horizontal line;
3) B=0, A≠0:
Ax + C =0, 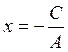 -
the vertical line;
-
the vertical line;
4) C=0: Aх + Ву =0 - passes through the origin.
1.3.
![]()
![]() - the direction
vector,
- the direction
vector,
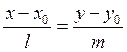 The
equation of the straight line, which
passes through the point M0(x0,y0)
and has the direction vector
The
equation of the straight line, which
passes through the point M0(x0,y0)
and has the direction vector ![]() :
:
1.4.
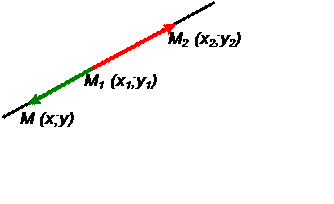
The equation of the straight line, which passes through the points M1(x1,y1) and M2(x2,y2):
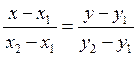 |
Example.
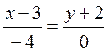 The
equation of the straight line, which
passes through the points М1(3;-2)
and М2(-1; -2):
The
equation of the straight line, which
passes through the points М1(3;-2)
and М2(-1; -2):
2. The angle between the straight lines

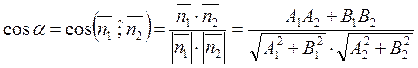 |
|||
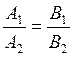 |
|||
The condition of parallelism of two straight lines:
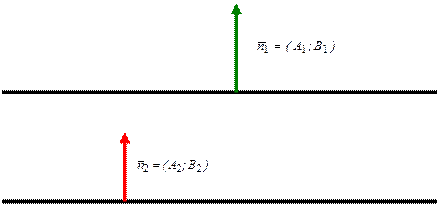
![]() The
condition of perpendicularity of two straight lines:
The
condition of perpendicularity of two straight lines:
![]()
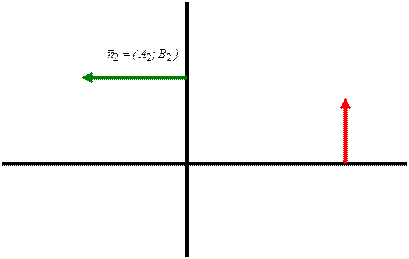
3. The distance from the point М0 (x0;y0) to the straight line Ax+By+C=0:
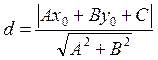
4. A circle is a locus of points, equidistant from the given point О, called a center of circle, at the distance R. A number R > 0 is called a radius of circle.
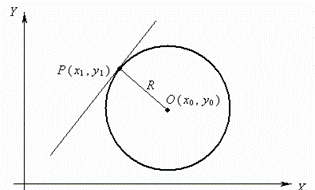
An equation of circle of radius R with a center in a point О ( х0 , у 0 ) is:
An ellipseis called a locus of points, a sum of distances from which to the two given points F1 and F2 , called focuses of ellipse, is a constant value.
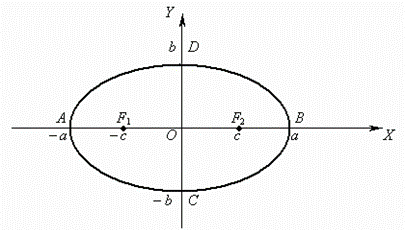
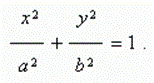
If a = b an ellipse becomes a circle ( in this case focuses of ellipse coincide with a center of circle ). Thus, a circle is a particular case of an ellipse.
Here the origin of coordinates is a center of symmetry of ellipse, and the coordinate axes are its axes of symmetry. a, b are called semiaxes.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.