Вища математика: Навчальний посібник (англійською мовою), страница 13

A minimum and the minimum value of the function are defined analogously.

The maximum and minimum of the function are called extrema of the function.

(Sometimes these points of extremum are called the points of local extremum.)

Assume that we have a function z = f(x, y) with domain D and our task is to test the given function for extrema.

Let’s consider the algorithm of this investigation.

At first let’s consider the necessary conditions of an extremum. These conditions are as follows: if the function z = f(x, y) attains an extremum at the point M₀(x₀,y₀), then its partial derivatives at this point either equal zero or do not exist.

So, if the partial derivatives at some point either equal zero or do not exist, then this point may be the point of extremum. It is called a critical point of function.

So, in practice we should equate tozero the partial derivatives and get the coordinates of the critical points from the system:

 

-  the critical point of function.

(I’d like to notice, that in simplest case we will have one critical point of function. But we should understand that systemmayhave no solutions or may have several solutions).

(The partial derivatives of function should be equal to zero and from this condition we get the critical points of function. We will say that the critical points are suspiciousof the extremum.)

After that let’s consider the sufficient conditions of an extremum. At first Let’s introduce the notation:

 

(These notations are commonly used)

So, the sufficient conditions are as follows:

1) if Δ>0 and A<0, then function has a maximum at the point M₀;

2) if Δ>0 and A>0, then function has a minimum at the point M₀;

3) if Δ<0, then function hasn’t an extremum at the point M₀, i.e. has neither maximum nor minimum at the point M₀ (in this case the point M₀ is called a saddle point);

4) if Δ=0, then function may have or may not have an extremum at the point M₀ (in this case an additional investigation is required – but itis not includedinourprogram).

Let’s consider some examples.

Example 1. Examine z=x²+y² for extrema.

Solution. Set up the system, equating tozerothe partial derivatives: .......

Get the coordinates of the critical points: .....

As we can see this function has one critical point: M₀(0;0).

It is suspiciousof the point of extremum.

Use the sufficient conditions of an extremum. Find the two-order partial derivatives of the function. Calculate its values at the critical point: ...

We got that Δ>0 and A>0. So, the function has a minimum at the point M₀(0;0). The minimum value equals 0. Really, substitute the coordinates of the critical point шт (штto)the function: ...

On the otherhand we cangetthe sameresult by considering the graph of function (as you know the graph of this function is elliptic paraboloid, exactly, paraboloid of revolution (rotation) (it is one of the second-order surface): ...

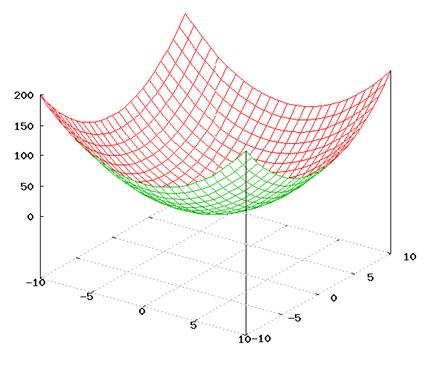
Example 2. Test the function z=x²-y² for extrema.

Set up the system, equating tozerothe partial derivatives: .......

Get the coordinates of the critical points: .....

As we can see this function has one critical point: M₀(0;0).

It is suspiciousof the point of extremum.

Use the sufficient conditions of an extremum. Find the two-order partial derivatives of the function. Calculate its values at the critical point: ...

We got that Δ<0. So, the function hasn’t an extremum at the point M₀, i.e. has neither maximum nor minimum at the point M₀(0;0).

On the otherhand we cangetthe sameresult by considering the graph of function (as you know the graph of this function is hyperbolic paraboloid: ...

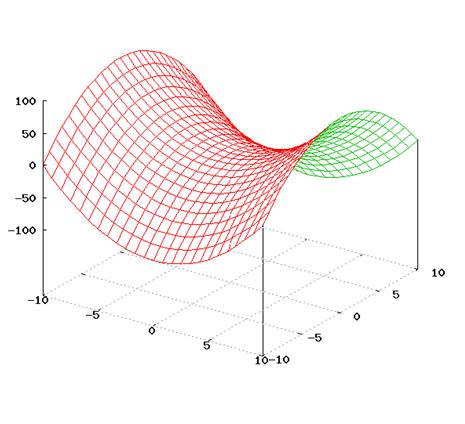
I suggest you to solve the next tasks on your own.

Example 3. Examine the next functions for extrema:

a) z=x²-xy+y²+3x-2y+1;

b) z=x³+y³-3xy;

c) z=3x²y-x³-y⁴.

The tasks b and c are the problems of high difficulty.

Example 4.

Assume that two types of goods are produced. Let it be known that:

p₁=$8,000 (8 thousand dollars) - the price of the first product,