Система активного контроля наружного диаметра штоков амортизаторов, страница 13

Для заполнения графы 4 необходимо установить значения  и С. В качестве величины  - начала отсчетов – можно принимать любое значение, но лучше всего принимать  равным Х_i, имеющим наибольшую частоту.Величина С есть величина разряда. Графа 5 представляет собой произведение данных графы 4 на данные графы 3; графа 6 – произведение данных   графы 5 и данных графы 4. далее необходимо подсчитать суммы по графам 3, 5 и 6.

Искомые значения и s определяются по формула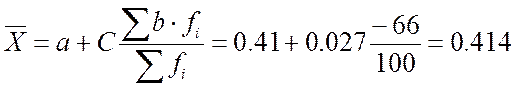м:

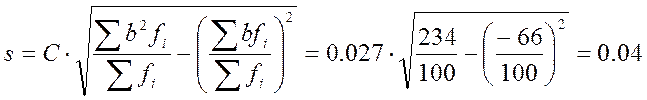 мм;

 мм.

Определение характеристик распределения при помощи моментов. Определение статистических характеристик эмпирических распределений целесообразнее производить при помощи моментов. Для вычисления моментов составляют вспомогательную таблицу, структуру которой и схему вычисления моментов с ее помощью покажем на примере таблицы 5. Она отличается от таблицы 4 дополнительными графами 6, 7, 8, 9, заполнение которых ясно из их заголовков и не требует пояснений. За начало отсчетов и здесь следует принимать =Х_i с наибольшей частотой. Здесь за начало отсчетов принята величина =0,41, величина разряда С=0.027, а величина 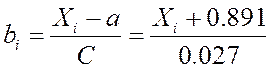. Первые семь столбцов служат для вычисления моментов, а последние два (8 и 9) – для проверки правильности вычисления начальных моментов.

Таблица 5  Вспомогательные данные для вычисления моментов

Пользуясь данными таблицы 5, вычислим начальные моменты:

;

;

;

.

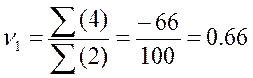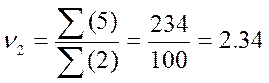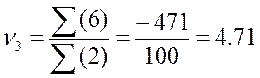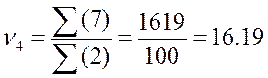Для проверки правильности вычисления первых четырех начальных моментов необходимо вычислить начальный момент относительно значения, передвинутого на один разряд от  в направлении убывающих значений по формуле:

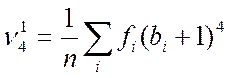, где .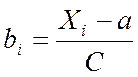

Если значение , вычисленное по этой формуле, совпадает со значением , вычисленным по формуле:

, то вычисления начальных моментов можно признать правильными. Подставляя в формулу 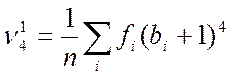 значения из  таблицы 5, получим: 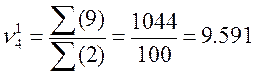. Следовательно начальные моменты вычислены правильно.

Для вычисления центральных моментов произведем предварительно вычисления следующих значений:

; ;

Тогда получим:

;

;

Для проверки правильности вычислений центральных моментов определим  и  по формулам:

;

Так как полученные значения  и  совпадают с ранее вычисленными, то, следовательно, вычисление центральных моментов произведено правильно.

Пользуясь моментами, вычислим статистические характеристики распределения:

;

;

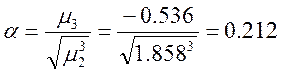; если (α>0) асимметрия положительная, если (α<0) ассиметрия отрицательная, если (α=0) асимметрия отсутствует,

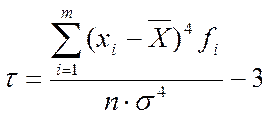
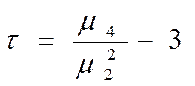
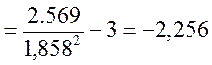
а (τ>0) вершина кривой лежит выше нормальной,

(τ<0) вершина кривой лежит ниже нормальной,

(τ=0) кривая нормальная.

Следовательно можно сделать вывод: (α>0) асимметрия положительная, а (τ>0) вершина кривой лежит выше нормальной.