Теоретическое и экспериментальное определение динамический характеристик передающей цепи и нахождение реакций на тестовые сигналы и сигнал заданной формы, страница 9

По энергетическому спектру входного сигнала (рис.22) определим граничную частоту спектра (эффективную полосу частот спектра входного сигнала)

.

Эффективная полоса частот спектра входного сигнала  полностью входит в полосу пропускания фильтра нижних частот , следовательно, энергия заданного импульсного сигнала эффективно проходит через цепь.

Расчет установившегося режима при несинусоидальном установившемся воздействии

 Определим выходную реакцию  на несинусоидальный установившийся импульс , где .

Согласно операторному методу расчета, , где ,  – операторная передаточная функция цепи (). Для нахождения оригинала  воспользуемся интегралом свертки

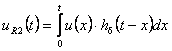
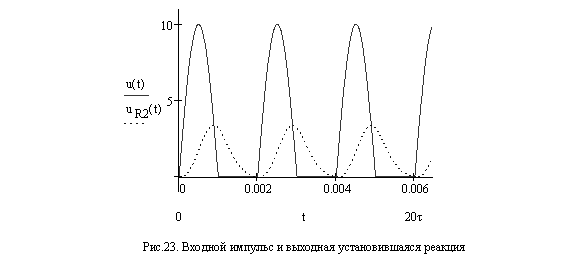
Выходную реакцию можно также восстановить по первым  гармоникам, представив входной импульс в виде тригонометрического ряда Фурье (19),

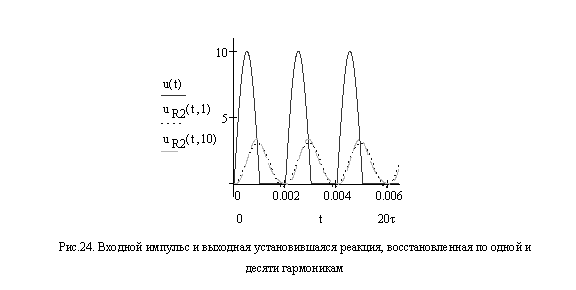
Определим основные характеристики периодического входного сигнала.

Скважность , где период следования импульсов, длительность импульсов. Скважность обратно пропорциональна коэффициенту заполнения и характеризует плотность заполнения периода колебания самим колебанием (импульсом).

Действующее значение

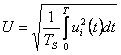
Среднее по модулю

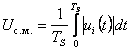
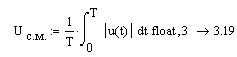
Коэффициент формы  и амплитуды

Коэффициент гармоник

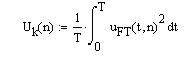
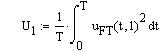
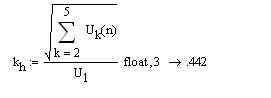
Экспериментальная проверка результатов расчетов

Для экспериментальной проверки результатов расчетов используем систему динамического моделирования Simulink, входящую в пакет MATHLAB, а также систему схемотехнического моделирования Multisim 2001.

На рис.25 представлена схема для экспериментального анализа цепи в системе Simulink. Моделирование цепи и решение дифференциальных уравнений (5) и (8), описывающих входную и выходную реакции, осуществляется в блоке State-Space, в который вводятся матрицы A, B, C и D параметров четырехполюсника.