Теоретическое и экспериментальное определение динамический характеристик передающей цепи и нахождение реакций на тестовые сигналы и сигнал заданной формы, страница 4

Переходной характеристикой четырехполюсника  является его реакция на входной сигнал в виде единичной ступенчатой функции Хевисайда .

Общий вид характеристического уравнения и его решение для рассматриваемого четырехполюсника имеют вид

,                                    (11)

где обобщенный коэффициент демпфирования (характеризует затухание амплитуды колебаний); ; . Определим корни характеристического уравнения

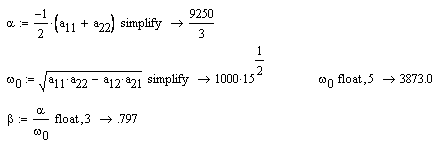
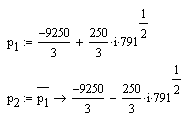
Обобщенный коэффициент демпфирования , следовательно, корни характеристического уравнения – комплектно-сопряженные, характер переходного процесса – переходной процесс проходит в режиме затухающих колебаний. Частота собственных колебаний  и постоянная времени  (или время релаксации – величина, имеющая размерность времени, характеризующая скорость протекания переходного процесса: за время  амплитуда колебаний уменьшается в  раз) равны

Переменные состояния цепи, , а так же входная и выходная реакции, , рассматриваются как сумма свободной и установившейся реакций: , . В режиме затухающих колебаний () свободная составляющая находится в виде

                                   (12)

где коэффициент затухания (величина обратно пропорциональная постоянной времени),  и постоянные интегрирования.

Определим переходные характеристики относительно переменных состояния  и

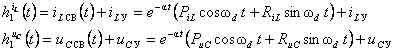                     (13)

Установившаяся составляющая переходной характеристики  равна

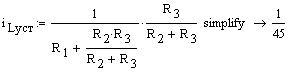
Установившаяся реакция переходной характеристики  равна

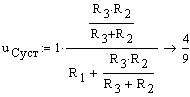
Определим постоянные интегрирования  и , используя начальные условия  и ,

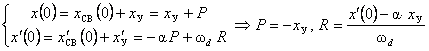                      (14)

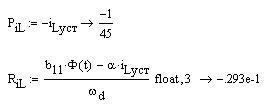
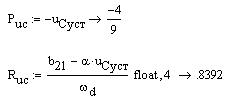
Теперь запишем выражения для переходных характеристик относительно переменных состояния и постоим их графики (рис.5)