Используя дифференциальные соотношения ![]() ,
, ![]() запишем
дифференциальные уравнения относительно переменных состояния
запишем
дифференциальные уравнения относительно переменных состояния
![]() (3)
(3)
![]() (4)
(4)
Запишем те же дифференциальные уравнения в матричной форме
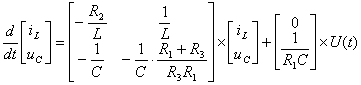 (5)
(5)
Запишем матрицы параметров ![]() и
и
![]()
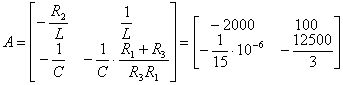 (6)
(6)
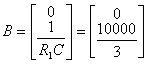 (7)
(7)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Запишем матричное уравнение для входной и выходной реакции
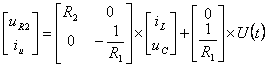 (8)
(8)
Запишем матрицы параметров ![]() и
и
![]()
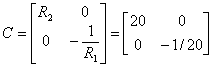 (9)
(9)
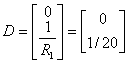 (10)
(10)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Проверим правильность составления матриц параметров ![]() ,
,![]() ,
,![]() ,
,![]() :
по схеме замещения для установившегося режима постоянного тока (рис.4,
:
по схеме замещения для установившегося режима постоянного тока (рис.4, ![]() ) определим установившиеся реакции и
сравним их с реакциями, найденными из уравнений (5) и (8) при условии
) определим установившиеся реакции и
сравним их с реакциями, найденными из уравнений (5) и (8) при условии ![]() (
(![]() ).
).

По схеме замещения (рис.4) находим
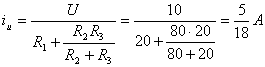 ;
;
![]() ;
;
![]() .
.
Из уравнения (5) с учетом ![]() по
формуле
по
формуле 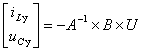 находим
находим
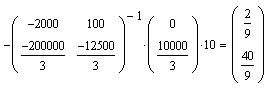
Из уравнения (8) находим ![]() и
и ![]()
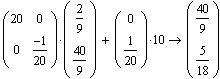
Как видно, найденные по формулам (5) и
(8) установившиеся реакции совпадают с реакциями, найденными по схеме замещения
(рис.4). Следовательно, матрицы параметров ![]() ,
,![]() ,
,![]() ,
,![]() и уравнения состояния
четырехполюсника составлены правильно.
и уравнения состояния
четырехполюсника составлены правильно.
Определение переходных характеристик путем решения дифференциальных уравнений
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.