Определение реакции цепи на импульсные сигналы
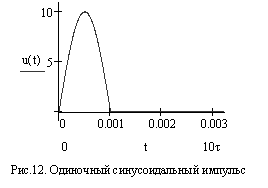 Определим реакцию цепи на одиночный синусоидальный импульс (рис.12).
Математически этот импульс можно представить с помощью единичной ступенчатой
функции Хевисайда:
Определим реакцию цепи на одиночный синусоидальный импульс (рис.12).
Математически этот импульс можно представить с помощью единичной ступенчатой
функции Хевисайда: ![]() , где
, где ![]() ,
, ![]() –длительность
импульса. Для определения реакции
–длительность
импульса. Для определения реакции ![]() используем
операторный метод: определим операторное изображение импульса и выходную
реакцию с помощью операторной передаточной функции по напряжению
используем
операторный метод: определим операторное изображение импульса и выходную
реакцию с помощью операторной передаточной функции по напряжению
![]()
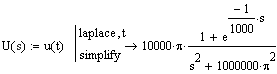
![]()
Оригинал операторной функции ![]() найдем
как свертку оригиналов функций
найдем
как свертку оригиналов функций ![]() и
и ![]() (или как интеграл наложения), где
(или как интеграл наложения), где ![]() – оригинал функции
– оригинал функции ![]() ,
, ![]() –
оригинал операторной передаточной функции
–
оригинал операторной передаточной функции ![]() и
одновременно импульсная характеристика, найденная ранее:
и
одновременно импульсная характеристика, найденная ранее:
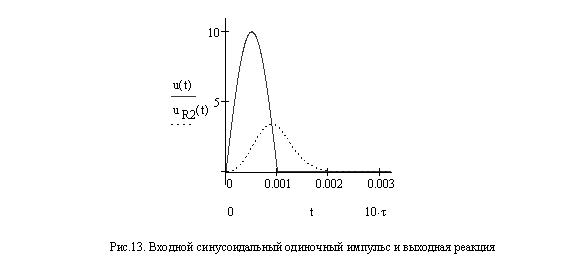
На рис.13 представлены входной синусоидальный импульс ![]() и выходная реакция
и выходная реакция ![]() .
.
Определим выходную реакцию на одиночный синусоидальный импульс с помощью интеграла Дюамеля
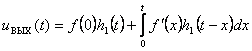 (18)
(18)
где ![]() ступенчатое
изменения сигнала в момент
ступенчатое
изменения сигнала в момент ![]() ,
, ![]() переходная характеристика цепи,
переходная характеристика цепи, ![]() производная входного импульсного
сигнала.
производная входного импульсного
сигнала.
Поскольку входной импульсный сигнал
не имеет ступенчатых скачков, то интеграл Дюамеля для выходной реакции ![]() запишется в виде
запишется в виде
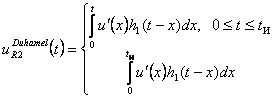
где ![]() –длительность
импульса.
–длительность
импульса.

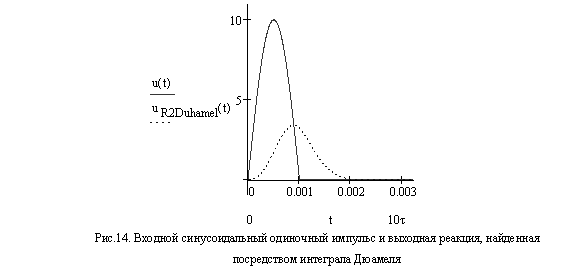
Как видно из рис.13 и рис.14, реакции на одиночный синусоидальный импульс, найденные с помощью операторной функции передачи цепи и с помощью интеграла Дюамеля, совпадают.
Построение частотных характеристик цепи
Спектр выходной реакции определяется с помощью комплексной
частотной характеристики цепи ![]() , которая
получается из операторной функции передачи по напряжению
, которая
получается из операторной функции передачи по напряжению ![]() при замене
при замене ![]()
![]() .
.
![]()
![]()



Модуль комплексной
частной характеристики ![]() является
амплитудно-частотной характеристикой цепи (рис.15), а аргумент
является
амплитудно-частотной характеристикой цепи (рис.15), а аргумент 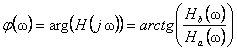 – фазочастотной характеристикой цепи
(рис.16).
– фазочастотной характеристикой цепи
(рис.16).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.