Теоретическое и экспериментальное определение динамический характеристик передающей цепи и нахождение реакций на тестовые сигналы и сигнал заданной формы, страница 5

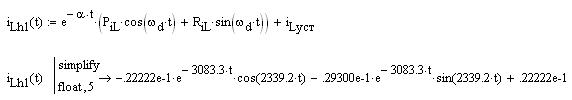
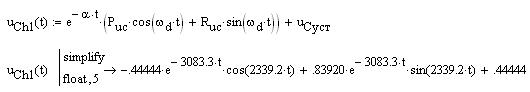
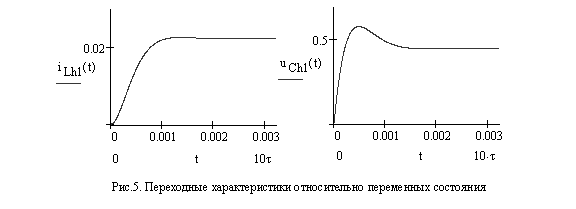
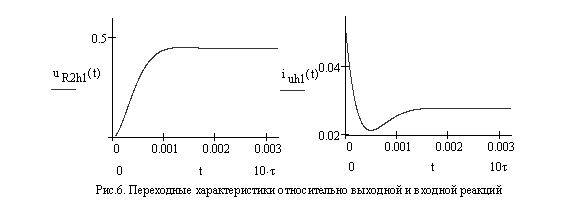
По формулам (8) определим переходные характеристики относительно выходной  и входной реакций и построим их графики (рис.6)

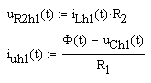
где Ф(t)=1(t) – единичная ступенчатая функция Хевисайда.

Определение переходных характеристик по схемам замещения

Характеристическое уравнение и его корни (11) можно также найти по схеме замещения (рис.6) при замене источника напряжения – КЗ, а L- и C-элементов – их сопротивлениям свободным токам  и .

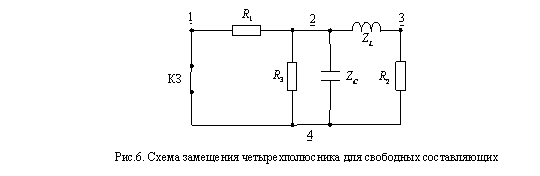
Найдем  относительно точек разрыва ветви, содержащей элемент КЗ,

                               (15)

 и его корни совпадают с характеристическим уравнением (11) и его корнями.

Определение импульсных характеристик четырехполюсника

Импульсной характеристикой цепи  называется реакция цепи на -импульс – импульсный сигнал с бесконечно малой длительностью, бесконечно большой амплитудой и площадью, равной единице. Дельта-функцию (она же – функция Дирака) математически можно представить так

                                      (16)

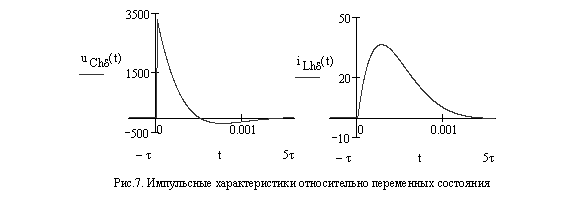
Во временной области импульсную характеристику  можно определить непосредственным дифференцированием переходной характеристики  с учетом начальных условий

                                                (17)

Тогда по формуле (17) получим

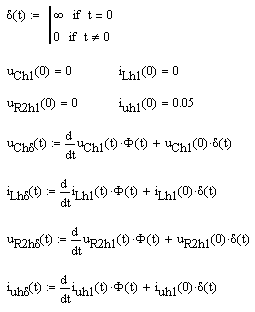
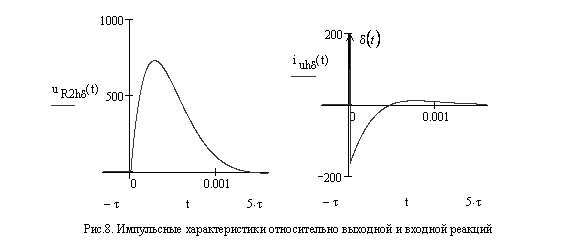
Графики импульсных характеристик выходной и входной реакций представлены на рис.8, -импульс обозначен стрелкой.  Графики импульсных характеристик относительно переменных состояния представлены на рис.7.

Определение реакций на линейное напряжение

Определим реакцию цепи  на сигнал  (). Так как корни характеристического уравнения комплексно-сопряженные, то свободная составляющая изменяется по закону .

Закон изменения установившейся реакции задается формой входного сигнала , где  и  – неизвестные коэффициенты, которые находятся из системы уравнений

,

где  и – матрицы параметров четырехполюсника (6) и (7);