Пути совершенствования системы оценки и управления ликвидностью банковской организации, страница 4

Так как расчетные значения коэффициентов, по сути, являются случайными величинами, то существует высокая вероятность того, что через определенный промежуток времени, например, полгода, год и выше (в зависимости от объема первоначальной выборки) вероятностные характеристики имеющейся совокупности могут измениться. Соответственно, изменению подвергнется и сам закон, которому подчиняются отдельные значения в совокупности. Сложность состоит не столько в том, что повторное определение закона потребует дополнительных затрат времени, сколько в самой интерпретации закона распределения вероятностей, так как колебания расчетных значений коэффициентов могут не подойти под описания общепринятых и наиболее распространенных законов распределения вероятностей.

В связи с описанным выше предлагается несколько упростить метод статистической оценки ликвидности коммерческого банка, перейдя от элементов теории вероятности к статистическим методам анализа.

Так, согласно общей теории статистики доверительный интервал для оценки средних значений по совокупности можно найти, используя следующую формулу [28, с70]:

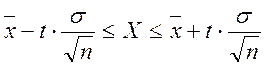, где (3.1.)

 - среднее значение по совокупности;

 - коэффициент доверия – табличные значения интегральной функции нормального распределения, соответствующие заданной вероятности. При заданной вероятности 80% t=1,5 [28, с70];

 - размер выборки;

 - стандартное отклонение по совокупности от среднего значения, рассчитываемое по формуле:

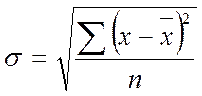(3.2.)

Тогда, для группы счетов до востребования:

;

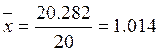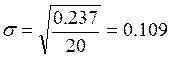
и доверительный интервал имеет вид:

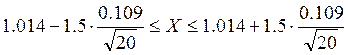
Таким образом, с вероятностью 0,8 можно утверждать, что значения показателя будут принадлежать промежутку [0,983;1,045].

Для группы срочных счетов клиентов в филиале:

;

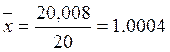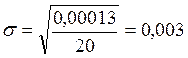
и доверительный интервал имеет вид:

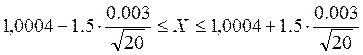
Таким образом, с вероятностью 0,8 можно утверждать, что значения показателя будут принадлежать промежутку [0,99954;1,00126]. Как видно из расчета, доверительный интервал минимально колеблется около единицы, что говорит о незначительном отклонении сальдо по счету на конец дня от размера средств на счету на начало дня.

Для группы счетов стандартных кредитов клиентам:

;

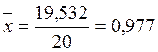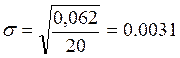
и доверительный интервал имеет вид:

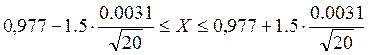
Таким образом, с вероятностью 0,8 можно утверждать, что значения показателя будут принадлежать промежутку [0,976;0,986], что уже говорит превышении суммы входящего сальдо на утро над исходящим к концу дня.

Как видно из табл. 3.1. границы доверительных интервалов при использовании в расчетах статистических методов сжимаются. Другими словами, интервал колебаний среднего значения из рассматриваемой совокупности уменьшается и соответственно увеличивается точность оценки основных тенденций в изменении значений показателя.

Таблица 3.1.

Сравнение полученных значений доверительных интервалов для коэффициента стабильности остатка в расчете с использованием методов математической статистики и общей теории статистики

В качестве значений показателей, используемых далее в методике оценки ликвидности, возьмем максимальное отклонение от среднего значения коэффициента стабильности остатка денежных средств по счетам денежных средств. То есть значение, соответствующее нижней границе рассчитанных доверительных интервалов.

Таким образом, на основании произведенных расчетов можно утверждать, что на конец рабочего дня на счетах до востребования в филиале будет находиться не менее 98,3% от сальдо на начало дня, то есть средства клиентов до востребования будут предъявлены к оплате в объеме не более 1,7%.