Расчет двухшарнирной арки

М-9. РАСЧЕТ ДВУХШАРНИРНОЙ АРКИ

9.0. Введение в модуль

Основной       целью      модуля      является       получение       формул                               для определения  внутренних  усилий  в  двухшарнирной  арке  от  неподвижной нагрузки.

Структура      изучаемого       модуля      включает      следующие       учебные элементы:

1. Применение метода сил для расчета двухшарнирной арки.

2. Определение       внутренних      усилий     в    двухшарнирной       арке    от неподвижной нагрузки.

3. Поверки правильности расчета двухшарнирной арки.

При   изучении   учебных   элементов   рекомендуется   использование следующей литературы – [3, c. 293 – 308]; [4, c. 366 – 370].

9.1. Применение метода сил для расчета двухшарнирной арки

9.1.1. Постановка задачи

Будем   рассматривать   двухшарнирную   арку   с   опорами   в   одном уровне                  и    имеющую      некоторое      симметричное      очертание      согласно

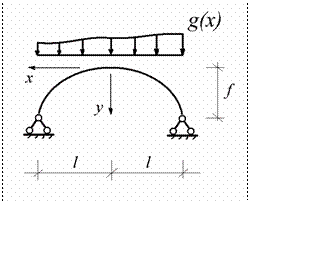заданному закону

y =  f ( x ) (рис.9.1)

Рис.9.1

Степень  полной  статической  неопределимости  заданной  двухшарнирной арки равняется

Л = 1

Поперечное  сечение  арки  имеет  переменные  размеры  по  длине  ее оси.          Изменения      геометрических       характеристик      поперечного          сечения (площадь,  момент  инерции)  вдоль  оси  арки  описываются  некоторыми заданными функциями

A = A(s );

I z   = I z

(s )

Геометрические      характеристики       в      замковом      сечении      имеют,

соответственно, значения

A0 ,

I0 .

На    арку    действует    произвольная    неподвижная                  вертикальная нагрузка,  показанная  на  рис.8.1        условно  как  распределенная  нагрузка  с переменной  интенсивностью. Ставится                  задача для               заданной      системы определить опорные реакции и внутренние усилия M, Q, N, возникающие в произвольном                  сечении             арки.    Заданная     система    считается    линейно деформируемой.

Двухшарнирные  арки  симметричного очертания с опорами  в одном уровне   имеют   широкое   распространение   в   строительной   практике,   а действующие   на   них   реальные   неподвижные   нагрузки,   как   правило, являются вертикальными.

9.1.2. Основная система и каноническое уравнение

Для   образования  основной   системы   метода   сил   необходимо   в заданной  системе  удалить  одну  лишнюю  связь  и  получить  статически определимую   систему.   Возможны   два   варианта   получения   статически определимой системы – балочный и арочный.

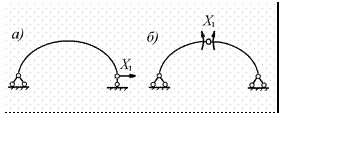Первый  вариант  связан   с   удалением   горизонтального                        опорного стержня  на  одной  из  опор  двухшарнирной  арки.  Полученная  статически определимая      система  представляет                        собой       кривой   брус,  опертый по балочной схеме (рис.9.2.а)

Рис.9.2

Второй   вариант    связан    с   введением   шарнира    в    замковое               сечение двухшарнирной  арки.  В  этом  случае  статически  определимой  системой является  трехшарнирная  арка  (рис.9.2.б).  Исходя  из  близости  восприятия нагрузок   трехшарнирной      и                    двухшарнирной    арками                        для  образования основной   системы,   выберем   второй   вариант   статически   определимой системы.

Статическая      эквивалентность       трехшарнирной    арки    заданной системе   достигается   приложением   к   ней   в   качестве   дополнительного

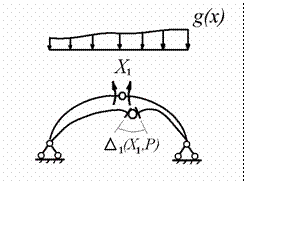внешнего воздействия реакции удаленной лишней связи

X1 , изгибающего

момента в замковом сечении двухшарнирной арки (рис. 9.3)

Рис.9.3

Эта реакция

X1   является основным неизвестным метода сил при расчете

двухшарнирной арки.

Кинематическая       эквивалентность        двух    систем                                            достигается введением требования обращения в нуль взаимного угла поворота торцов в замковом шарнире

,P ) = 0

(9.1)

Данное перемещение вызвано основным неизвестным и заданной внешней нагрузкой.

Трехшарнирная   арка,   для   которой   соблюдаются   требования                                       ее статической  и  кинематической  эквивалентностей  с  заданной  системой  и является основной системой метода сил для двухшарнирной арки.

Основная     система,      как      и     заданная,      считается                               линейно- деформируемой  системой.  Поэтому,  согласно  принципу  суперпозиции, взаимный  угол поворота  торцов в  замковом  шарнире  будет  складываться

D1 X   ,   вызванного    действием    основного