Расчет двухшарнирной арки, страница 3

Знак  минус  говорит  о  том,  что  единичный  распор  направлен  наружу  от контура арки.

С    учетом    полученных    величин    опорных    реакций                единичные внутренние  усилия  в  произвольном  сечении  описываются  следующими формулами:

-   единичный изгибающий момент

m1  =

1 × ( f f

- y )

(9.8)

-   единичная поперечная сила

q1  =

1 × sinj

f

(9.9)

-   единичная продольная сила

n1  =

1× cosj

f

(9.10)

С   целью   определения   внутренних   усилий   от   заданной   нагрузки

M P , N P

образуем   грузовое    состояние,    нагружая    основную    систему

заданной нагрузкой (рис.9.5)

Рис.9.5

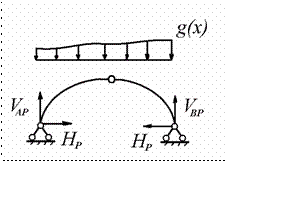Опорные реакции

VAP ,VBP ,H P

и внутренние усилия

M P , QP , N P

в грузовом

состоянии    определяются    по    формулам,   полученным       для                     расчета трехшарнирной арки при действии неподвижной вертикальной нагрузки в модуле М-5 первой части курса.

Так как единичные внутренние усилия

m1 ,

n1   и грузовые внутренние

усилия

M P , N P

всегда описываются нелинейными функциями, а их эпюры

имеют    криволинейное    очертание,    то     при  вычислении    интегралов, входящих   в   формулу   Максвелла-Мора   нельзя   пользоваться   правилом Верещагина.  В  этом  случае  для  их  вычисления  необходимо  применять численные методы. Такие методы основаны на приближенном вычислении площади  графика  подынтегральной  функции.  Применим  для  вычисления определенных               интегралов,          входящих     в     формулы     (9.5),   (9.6),               метод трапеций.

С  этой  целью  осуществим  следующие  преобразования  в  формулах

(9.5),  (9.6).  Так  как  единичные  и  грузовые  внутренние  усилия  зависят  от абсциссы сечения x, то с помощью подстановки

ds =

dx

cosj

прежде    всего,    поменяем    переменную    интегрирования.   Кроме                того, подставим в них единичные внутренние усилия (9.8) и  (9.10). И, наконец, умножим и      поделим  первые   интегралы      этих                формул             на    изгибную

жесткость  замкового  сечения жесткость замкового сечения

EI0 ,  а  вторые  интегралы  -  на  продольную

EA0 .

вид

С учетом проделанных преобразований формулы (9.5) и (9.6) примут

( ò F dx + r 2 ò F dx )

(9.11)

и

D     =     1

(   F dx + r 2

F dx )

(9.12)

1 P           f

ò   1

EI0     2 l

0   ò   2

2 l

где

F  = (f

- y )M P

EI0,  F   = N

EA0,  F

= EI0( f

- y )2

,  F

= EA0cosj ,

1cosj        EI

2              P    EA

3EI

cosj

4EA

r 2=

I0.  Следовательно,  все  интегралы,  входящие  в  (9.11),  (9.12),  можно

0

записать одинаково

Ik= ò Fkdx

2l

(k = 1,...,4)

и использовать для их вычисления формулу метода трапеций

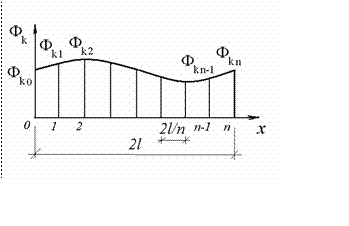kn ⎝ 2    k0

k1  + ... + F

kn -1

+ 1 F

2

⎞

kn  ⎟

⎠

(9.13)