Расчет двухшарнирной арки, страница 2

неизвестного,   и   частичного   перемещения

D1P ,   вызванного   действием

нагрузки. Следовательно, условие (9.1)  примет вид

D

1P

1 X1

+ D   = 0

(9.2)

1

Так   как   изменения   частичного   перемещения

D1 X         и   основного

неизвестного

X1   связаны прямой пропорциональной зависимостью, то

1 X              11      1

D    = d  X  ,                                                (9.3)

1

d

где    11

- единичный взаимный угол поворота торцов в замковом шарнире

~

основной системы от действия безразмерного момента

X1  = 1.

С учетом (9.3) условие (9.2) примет вид уравнения

d   X   + D

11        1              1P   = 0

(9.4)

Полученное   уравнение    (9.4)   и   является   каноническим      уравнением метода  сил  для  двухшарнирной  арки.  Для  его  решения  и  нахождения

основного   неизвестного

X1     необходимо   определить   коэффициент   при

d

основном  неизвестном    11

D1P .

и  свободный  член  канонического  уравнения

9.1.3. Особенности определения коэффициента и свободного

члена

Поскольку  коэффициент  при  основном  неизвестном  и  свободный член  канонического  уравнения  являются  перемещениями,  возникающими в   трехшарнирной   арке   от   нагрузки   (соответственно,   единичной   или заданной), то для их определения используется формула Максвелла-Мора.

11

Эта формула для определения единичного перемещения d

имеет вид

n

m

2

d

= ò

11

1   ds + ò

2

1   ds

(9.5)

s   EI z

s   EA

D

а при определении перемещения от действия нагрузки     1P

принимает вид

1P        ò             ò

D    =   m1M P ds +

n1 N P ds

(9.6)

s      EI z

s     EA

Из  формул  (9.5),  (9.6)  следует,  что  при  определении  коэффициента  и свободного          члена           необходимо                      учитывать                   влияние,      как             изгибающих моментов, так и продольных сил. Интегрирование в этих формулах ведется по длине оси арки.

Для   нахождения   коэффициента    при   основном   неизвестном   по

формуле (9.5) нужно определить единичные внутренние усилия

m1 , n1 . Для

нахождения свободного члена канонического уравнения по формуле (9.6),

кроме  того,  нужно  определить  внутренние  усилия  от  заданной  нагрузки

M P , N P .

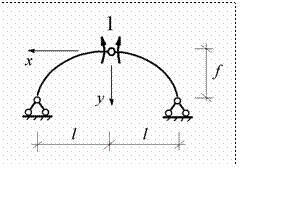С целью определения единичных внутренних усилий

m1 , n1

образуем

единичное     состояние,    загружая     основную     систему     безразмерным

~

моментом

X1  = 1 (рис.9.4)

Рис.9.4

В     опорных      закреплениях      единичного      состояния      вертикальные составляющие опорных реакций не возникают, а единичный распор равен

h = - 1

f

(9.7)