Расчет двухшарнирной арки, страница 5

Тогда,   применяя    принцип    суперпозиции,    получим   следующие формулы для определения в двухшарнирной арке опорных реакций

0

и внутренних усилий

VB   = VBP

H= MC   - X 1

f

M= m1 X 1  + MP

Q= q1 X 1  + QP

N = n1 X 1  + N P

9.3. Поверки правильности расчета двухшарнирной арки

Для   проверки    правильности   определения    опорных    реакций                    и внутренних                                усилий      выполняют                    две             поверки                      –             статическую                    и кинематическую.

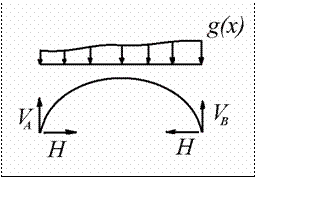Статическая  поверка  заключается  в  проверке  равновесия  арки  в целом при действии на нее заданной нагрузки и опорных реакций (рис.9.7)

Рис.9.7

С этой целью составляются три уравнения равновесия

å MA  = 0

å MB   = 0

å y = 0

(9.22)

Кинематическая    поверка    заключается    в    проверке    соблюдения условия для  замкового сечения двухшарнирной арки

которое с учетом формулы Максвелла-Мора принимает вид

mM           n N

ò       1         ds+ ò     1       ds= 0

(9.23)

s     EI z

s    EA

Выполнив     с     левой     частью     (9.23)     преобразования,     аналогичные преобразованиям формул (9.5), (9.6), получим

2

где

ò F5 dx + r0

2 l

ò F6 dx = 0

2 l

(9.24)

- y)M

EI0

EI

F   = NEA0

6                 EA

Применяя для вычисления интегралов, входящих в (9.24), формулу метода трапеций, получим окончательное выражение для кинематической поверки

Входящие в (9.25) S5

и S6

S5  + r0  S6  = 0

вычисляются по формуле (9.14).

(9.25)

При   выполнении    условий   (9.22)   и   (9.25)   опорные   реакции   и внутренние усилия считаются найденными правильно.

9.5. Резюме

При расчете двухшарнирной арки   методом   сил   предпочтительным вариантом основной системы является трехшарнирная арка.

При  определении  коэффициента  и  свободного  члена  канонического уравнения  метода  сил  по  формуле  Максвелла-Мора  нельзя  пользоваться правилом Верещагина. Для вычисления интегралов, входящих в формулу Максвелла-Мора используются численные методы.

Для    определения     внутренних    усилий    внутренних    усилий                    в двухшарнирной        арке       согласно       принципу                    суперпозиции   складываются внутренние              усилия,                    найденные        в         трехшарнирной  арке          от  основного неизвестного  и заданной нагрузки.

Для   проверки   правильности    полученных    значений    внутренних усилий выполняется статическая и кинематическая поверки.

9.6. Материалы для самоконтроля

Проверьте,   как   Вы   усвоили   следующие   понятия,   определения, алгоритмы и формулы:

-   заданная система;

-   основная система метода сил;

-   каноническое уравнение метода сил;

-   формула   для   определения   коэффициента   канонического   уравнения метода сил;

-   формула для определения свободного члена канонического уравнения;

-   формулы для определения внутренних усилий в единичном состоянии;

-   формулы для определения окончательных внутренних усилий;

-   поверки правильности расчёта двухшарнирной арки.

Проверьте, можете ли Вы вывести:

-   уравнения и формулы для расчёта двухшарнирной арки.