М-12. ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
12.0. Введение в модуль
Основными целями модуля являются:
- введение понятий конечного элемента и узла;
- рассмотрение типов конечных элементов и их характеристик;
- получение матриц жесткости одномерного конечного элемента.
- получение матрицы жесткости конструкции;
- описание общей схемы применения метода конечных элементов.
Структура изучаемого модуля включает следующие учебные элементы:
1. Общие сведения о методе конечных элементов.
2. Расчет стержневых конструкций методом конечных элементов в форме метода перемещений.
При изучении учебных элементов рекомендуется использование следующей литературы: [3, c.435 - 493]; [5, c.466 - 514].
12.1.Общиесведенияо методе конечных элементов
12.1.1.Суть метода и его разновидности
Основная идея метода конечных элементов состоит в том, что рас- считываемая строительная конструкция заменяется совокупностью неко- торых элементов, соединенных между собой и с основанием в конечном числе точек. Элементы, на которые разбивается строительная конструкция, называются конечными элементами, а точки их соединения - узлами. При этом внешняя нагрузка заменяется системой эквивалентных узловых сил. Такая дискретизация исходной конструкции и действующей нагрузки позволяет заменить ее расчет расчетом некоторой идеализированной сис- темы с конечным числом степеней свободы.
Конечные элементы должны обладать постоянными жесткостными параметрами, а их напряженно-деформированное состояние должно с дос- таточной точностью описываться некоторыми аналитическими выраже- ниями. Это важно для определения связи между узловыми усилиями и пе- ремещениями.
В зависимости оттого, что принимается за неизвестные величины в узлах принято различать следующие разновидности метода конечных эле-
ментов. Если за основные неизвестные принять узловые усилия взаимо- действия между элементами, то это соответствует методу конечных эле- ментов в форме метода сил. Если в качестве основных неизвестных при- нять перемещения в узлах, то это соответствует методу конечных эле- ментов в форме метода перемещений.
В настоящее время метод конечных элементов является одним из наиболее распространенных численным методом, применяемым для расчета любых строительных конструкций и сооружений. Причем в расчетной практике преимущественно используется метод конечных элементов в форме метода перемещений.
12.1.2.Типы конечных элементов и их характеристики
По геометрической форме различают три типа простейших базовых конечных элемента, на которые могут разбиваться различные конструк- ции:
- одномерные;
- двухмерные;
- трехмерные.
Одномерный конечный элемент представляет
собой призматиче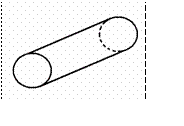 ский стержень (рис.12.1)
ский стержень (рис.12.1)
Рис.12.1
Двухмерный конечный элемент
может быть
двух видов - тре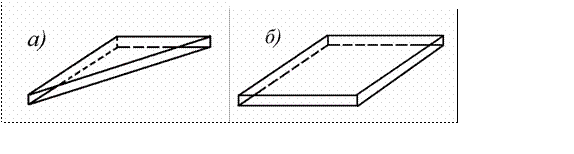 угольная пластина (рис.12.2.а) и прямоугольная пластина
(рис.12.2.б)
угольная пластина (рис.12.2.а) и прямоугольная пластина
(рис.12.2.б)
Рис.12.2
Трехмерный конечный элемент представляет собой тетраэдр
(рис.12.3)
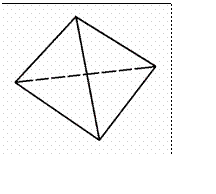 Рис.12.3
Рис.12.3
Наряду с перечисленными простейшими конечными элементами в качестве конечных элементов могут использоваться другие элементы бо- лее сложной геометрической формы. Такими элементами могут быть лю- бые геометрически неизменяемые части конструкции, для которых воз- можно получение зависимостей, описывающих их напряженно- деформированное состояние.
Конечные элементы характеризуются числом узлов и числом узло- вых реакций. Число узлов конечного элемента зависит от его формы и мерности. Например, число узлов у одномерного конечного элемента рав- няется двум, у двухмерного конечного элемента в виде треугольной пла- стины – трем, а виде четырехугольной пластины – четырем. Число узловых реакций у конечного элемента одного и того же типа может быть различ- ным и зависит от вида его напряженного состояния.
Рассмотрим наиболее характерные случаи напряженного состояния одномерного конечного элемента, которые могут встречаться при расчетах конструкций, и выясним, как, в зависимости от этого, может изменяться число узловых реакций.
Одномерный конечный элемент, работающий на растяжение-сжатие Такой конечный элемент характеризуется двумя узловыми реакциями. В каждом узле возникает одна реакция - продольная сила.
Одномерный конечный элемент, работающий на кручение. Такой конечный элемент также характеризуется двумя узловыми реакциями, но узловыми реакциями являются скручивающие моменты.
Одномерный конечный элемент, работающий на плоский изгиб в вертикальной плоскости или в горизонтальной плоскости. Число узловых
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.