Основы метода конечных элементов, страница 3

⎜ R

⎟

j 3 ⎟

⎜ R j 4 ⎟

⎜    j 5 ⎟

⎝    j 6 ⎠

а  напряженное  состояние  конструкции  в  целом  описывается  вектором

внутренних узловых усилий

⎛ R  ⎞

⎜   1  ⎟

⎜  M  ⎟

R = ⎜ R  ⎟

⎜    j  ⎟

(12.2)

⎜  M  ⎟

⎜   ⎟

⎝ RN  ⎠

Вектор  узловых  перемещений  (12.1)  и  вектор  внутренних  узловых усилий    (12.2)    характеризуют      напряженно-деформированное               состояние конструкции. При использовании метода перемещений они связаны между собой следующей линейной зависимостью

R = (k ) q

где (k ) - матрица жесткости конструкции.

Матрица жесткости конструкции имеет блочную структуру

(12.3)

⎛ (k  )   K

(k   )⎞

11

1N     ⎟

(12.4)

⎟

Каждый  блок  матрицы  жесткости  конструкции  представляет  собой  подматрицу единичных реакций, возникающих в произвольном узле, и, в общем случае, имеет размеры 6х6

⎛ k

K   k j1 f 6  ⎞

⎜

L  ⎟  ( j , f

= 1,..., N )

⎝ k j 6 f 1

K   k j 6 f 6 ⎠

Поскольку  в  качестве  неизвестных  величин  для  рассматриваемой разновидности  метода  конечных  элементов  принимаются  узловые  пере- мещения,  то  основными  уравнениями  будут  условия  равновесия  узловых точек.  Условия  равновесия       отдельных  узлов  конструкции  описываются соотношениями

Rj  - Qj   = 0

( j = 1,..., N )

а условия равновесия для конструкции в целом имеют вид

R- Q= 0

Тогда с учетом зависимости (13.13) условия равновесия конструкции примут  вид

(k) q- Q= 0

(12.5)

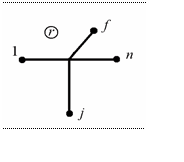12.2.3. Матрица жесткости конструкции

Деформированное состояние отдельного конечного элемента номера

r (рис.12.7)

Рис.12.7

в  произвольном  узле  j  характеризуется  собственными  линейными    пере-

мещениями

qr   ,qr

,qr

и угловыми перемещениями

qr   ,qr

,qr

и, следова-

j1       j 2        j 3

j 4       j 5        j 6

тельно, описывается вектором

⎛ qr    ⎞

⎜ qr    ⎟

q r   = ⎜

j 3 ⎟

j 4

⎜   r    ⎟

⎜ q j 5 ⎟

⎜ qr    ⎟

⎝    j 6 ⎠

Тогда деформированное состояние в целом отдельного конечного элемента, имеющего n узлов,  будет описываться вектором перемещений

⎛ qr  ⎞

⎜  1   ⎟

⎜  M  ⎟

qr   = ⎜ qr  ⎟

⎜   j  ⎟

⎜  M  ⎟

⎜   r  ⎟

⎝ qn  ⎠

В  соответствии  с  принятой  схемой  деформирования  отдельного  конечного элемента его напряженное состояние в произвольном узле j будет

характеризуется  тремя  силовыми  реакциями

Rr  ,Rr

,Rr

и  тремя  момент-

j1        j 2         j 3

j 5        j 6

и описывается вектором

⎛ Rr   ⎞

⎜ Rr    ⎟

R r   = ⎜

j 3 ⎟