Основы метода конечных элементов, страница 6

⎜ ki +111i1

ki +11i 2

ki +11i +11

ki +11i +12  ⎟

⎜   r                     r                     r                        r              ⎟

⎝ ki +12 i1

ki +12 i 2

ki +12 i +11

ki +12 i +12 ⎠

С  учетом  значений  единичных  реакций,  полученных  с  помощью  единичных эпюр, матрица (12.15) имеет вид

⎛ 12              6

⎜

⎜ a3                           a2

- 12

a3

6   ⎞

⎟

a2     ⎟

⎜

4              - =6

a                 a2

12

=2   ⎟

a   ⎟

6 ⎟

(12.16)

⎜                                       3

⎜                                    a

⎜        симметрично

⎝

-   2  ⎟

a  ⎟

4   ⎟

a   ⎠

При  плоском  изгибе  одномерного  конечного  элемента  в  горизонтальной

плоскости в (12.16) изгибная жесткость

EI z

заменится на

EI y .

Для  одномерного  конечного  элемента,  работающего  на  кручение,

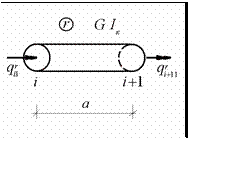деформированное  состояние  в  каждом  узле  характеризуется  одним  перемещением (рис.12.10)

Рис.12.10

Тогда вектор (12.11) принимает вид

⎛  qr    ⎞

q r   = ⎜

i1   ⎟

r

а матрица (12.12) принимает вид

⎝ qi +11 ⎠

(k )r

r

k r

r

(12.17)

⎝  i +11i1

i +11i +11 ⎠

С  учетом  значений  единичных  реакций,  полученных  с  помощью  единичных эпюр, матрица (12.17) имеет вид

(k )r

= GIк

a

⎛ 1

⎜

⎝ - 1

- 1⎞

⎟

1 ⎠

(12.18)

Для различных случаев сложного напряженного состояния, получае- мого вследствие совместного учета растяжения-сжатия, плоского изгиба и кручения,  матрицы  жесткости  получаются  объединением  соответствую- щих элементов матриц (12.14), (12.16), (12.18).

12.2.4. Матрица преобразования координат

При  выводе  формулы  (12.10),  позволяющей  формировать  матрицу жесткости конструкции из матриц жесткости конечных элементов, неявно предполагается, что конструкция и ее конечные элементы относятся к об- щей системе координат. В случае несовпадения систем координат необхо- димо  осуществлять  преобразование  матриц  жесткости  конечных  элемен- тов.

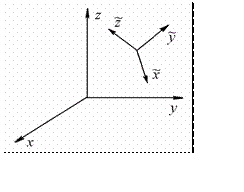Рассмотрим  две  координатные  системы  –  общую  x,  y,  z  и  местную

~x , ~y , ~z

(рис.12.11)

Рис.12.11

Общаякоординатнаясистемаиспользуется для получения матрицы же- сткости конструкции в целом, а местная координатная система – для по- лучения матриц жесткости отдельных конечных элементов.

Известно,  что  переход  от  одной  координатной  системы  к  другой можно  осуществлять  с  помощью  некоторой  матрицы  преобразования

координат(T ) . Для  конечных  элементов такая  матрица является  ортогональной, и она позволяет связывать векторы узловых перемещений

и векторы узловых реакций

= (T)qr,

= (T )R r,

qr= (T)¢ q~r

R r= (T )¢ R ~r

(12.19)

(12.20)

в общей и местной координатной системах.

Тогда из (12.20) с учетом зависимостей (12.6), (12.19)   можно полу- чить следующую формулу для определения матрицы жесткости конечного элемента при переходе от местной координатной системы к общей системе

(k )r= (T )¢(k )~r(T )

(12.21)

В общем случае напряженно-деформированного состояния, характеризуемого  12 узловыми перемещениями, структура матрицы преобразования координат (T ) определяется из зависимости (12.19) и имеет вид