Основы метода конечных элементов, страница 5

r

⎜ å (kN 1 )

⎝ rÎN ,1

K     å (kNN

rÎN ,N

)r  ⎟

⎠

Полученную  матрицу  жесткости  необходимо  подчинить  условиям  опира- ния конструкции. Для этого из нее необходимо исключить строки и столб- цы,  соответствующие  узловым  перемещениям,  по  направлению  которых наложены кинематические связи.

12.2.3. Матрицы жесткости одномерного конечного элемента

Деформированное    состояние    одномерного    конечного    элемента, имеющего два узла (рис.12.1),  в общем случае описывается вектором

⎛ qr   ⎞

q

r   = ⎜ i    ⎟

r

(12.11)

⎝ qi +1 ⎠

q

и

i

Элементами вектора (12.11) являются векторы узловых перемещений                    r

r

qi +1 . Тогда соответствующая (12.11) матрица жесткости конечного элемента будет иметь следующую структуру

⎝

(k )r   = ⎜

)

)

(k

ii                       ii +1        ⎟

(12.12)

(k  )     (k    )

⎛        r                  r    ⎞

⎜ (k

r

i +1i

r  ⎟

i +1i +1     ⎠

Элементами  матрицы  (12.12)  являются  подматрицы  единичных  узловых реакций. Размеры элементов (12.11) и (12.12) могут быть различными в за- висимости  от  вида  напряженного  состояния  одномерного  конечного  эле- мента.

Для одномерного конечного элемента, работающего на растяжение- сжатие, деформированное состояние в каждом узле характеризуется одним перемещением рис.(12.8)

k

Рис.12.8

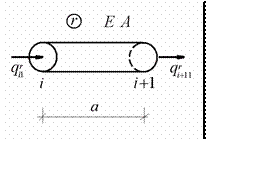
Тогда вектор (12.11) принимает вид

⎛  qr    ⎞

qr   = ⎜

i1   ⎟

r

а матрица (12.12) принимает вид

⎝ qi +11 ⎠

⎜

(k )r   = ⎛

r

i 1i 1

k

r

r

⎞

i 1i +11   ⎟

r

(12.13)

⎝ ki +11i 1

ki +11i +11 ⎠

Элементы  матрицы  (12.13)  являются  единичными  узловыми  реак-

k

циями. Так, например,

r

i1i1

- это реакция в i –том узле конечного элемента,

вызванная перемещением на единицу этого же узла в продольном направ-

k

лении, а

r

i1i +11

- это реакция в i –том узле конечного элемента, вызванная

перемещением  на  единицу  узла  i+1  в  продольном  направлении.  Точно

k

также два других элемента

r

k

и

i +1i1

r

i +11i +11

характеризуют реакции в i+1–том

узле,  обусловленные  соответствующими  единичными  перемещениями.  С учетом значений перечисленных единичных реакций, полученных с помо- щью единичных эпюр, матрица (12.13) имеет вид

r          EA ⎛ 1

- 1⎞

(k ) =

⎜           ⎟

a  ⎝ - 1    1 ⎠

(12.14)

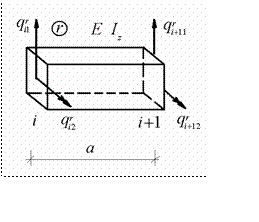
Для  одномерного  конечного  элемента,  работающего  на  плоский  из- гиб в вертикальной плоскости, деформированное состояние в каждом узле характеризуется двумя перемещениями (рис.12.9)

Рис.12.9

Тогда вектор (12.11) принимает вид

q

⎛     r    ⎞

q

r

⎜    i1   ⎟

r          ⎜    i 2   ⎟

q   = ⎜ qr                         ⎟

⎜  i +11 ⎟

⎜   r         ⎟

а матрица (12.12) принимает вид

⎝ qi +12 ⎠