Основы метода конечных элементов, страница 2

реакций такого конечного элемента уже равно четырем. В каждом узле появляется по две реакции - поперечная сила и изгибающий момент.

Одномерный конечный элемент, работающий на растяжение-сжатие и на плоский изгиб в вертикальной плоскости  или в горизонтальной плос- кости.  Такой  конечный  элемент  характеризуется  шестью  узловыми  реак- циями. В каждом узле возникает по три реакции – одна продольная и по- перечная силы и один изгибающий момент.

Одномерный конечный элемент, работающий на растяжение-сжатие, на кручение и изгиб в двух взаимно перпендикулярных плоскостях. Число узловых реакций у такого конечного элемента увеличивается до двенадцати. В каждом узле появляется по шесть реакций – одна продольная и две поперечных силы, один скручивающий и два изгибающих момента.

12.2.Расчетстержневыхконструкций методом конечных элементов в форме метода перемещений

12.2.1. Постановка задачи

Рассмотрим   произвольную   пространственную   стержневую   конст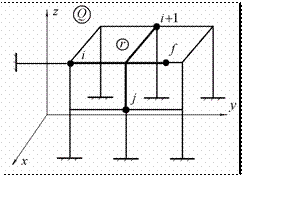рукцию (рис.12.4)

Рис.12.4

для которой считаются известными все размеры геометрической  схемы и поперечных  сечений  стержней.  Геометрическая  схема  конструкции  отне- сена к декартовой координатной системе.

На  заданную  конструкцию  действуют  произвольная  нагрузка,  пока- занная на рис.12.4 условным буквенным обозначением Q. Заданная конст- рукция  считается  линейно  деформируемой  системой.  Разобьем  конструк- цию на конечные элементы, которые могут иметь произвольную геометри-

ческую форму. Пусть число элементов равняется Mи они соединены между собой в N узлах.

Считаем,  что  заданная  произвольная  нагрузка  заменена  эквивалент- ной узловой нагрузкой. Схема составляющих такой нагрузки в произволь- ном узле, в принятой координатной системе, показана на рис.12.5

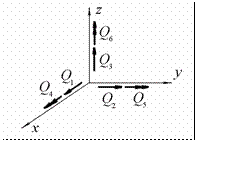Рис.12.5

Векторы с одинарной стрелкой соответствуют узловым силам, а векторы с двойной  стрелкой  –  узловым  моментам.  Тогда  эквивалентная  узловая  на- грузка  для  конструкции  в  целом                    описывается  следующим  вектором  на- грузки

⎛ Q  ⎞

⎜    1  ⎟

⎜  M  ⎟

Q = ⎜ Q  ⎟

⎜    j  ⎟

⎜  M  ⎟

⎜   ⎟

Здесь

⎝ QN  ⎠

⎛ Qj1  ⎞

⎜    ⎟

⎜ Qj 2 ⎟

⎜ Q

⎟

j 3 ⎟

⎜ Qj 4 ⎟

⎜    j 5 ⎟

⎝    j 6 ⎠

вектор нагрузки произвольного j-того узла (j=1,…,N).

Эквивалентная  узловая  нагрузка  в  общем  случае  определяется  сле- дующим  образом. Для каждого  конечного  элемента из условия равенства возможных  работ  заданной  нагрузки,  действующей  на  элемент,  и  неиз-

вестных  узловых  сил  определяются  эквивалентная  узловая  нагрузка  для конечного  элемента..  Тогда  эквивалентная  узловая  нагрузка  для  произ- вольного узла конструкции получается суммированием эквивалентных уз- ловых нагрузок по всем элементам, сходящимся в этом узле.

12.2.2. Условия равновесия конструкции

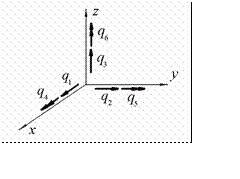
Деформированное  состояние  конструкции  в  произвольном  узле  j  в принятой координатной системе характеризуется тремя линейными   пере- мещениями  qj1,  q12,  qj3         и  тремя  угловыми  перемещениями  qj4,  q15,  qj6 (рис.12.6)

Рис.12.6

и, следовательно, описывается вектором следующего вида

⎛ q j1 ⎞

⎜   ⎟

⎜ q j 2 ⎟

⎜ q

⎟

j 3 ⎟

⎜ q j 4 ⎟

⎜    j 5 ⎟

⎝    j 6 ⎠

На  рис.  12.6  векторы  с  одинарной  стрелкой  соответствуют  линейным  пе- ремещениям, а векторы с двойной стрелкой – угловым перемещениям уз- лов. Тогда деформированное состояние конструкции в целом будет описы- ваться вектором перемещений

⎛ q  ⎞

⎜   1  ⎟

⎜  M  ⎟

q = ⎜ q  ⎟

⎜    j  ⎟

(12.1)

⎜  M  ⎟

⎜  ⎟

⎝ qN  ⎠

Согласно принятой схеме деформированного состояния конструкции ее напряженное состояние в произвольном узле j будет характеризоваться тремя  силовыми  реакциями  Rj1,  R12,  Rj3                            и  тремя  моментными  реакциями

Rj4, R15, Rj6   и описывается вектором

⎛ R j1  ⎞

⎜    ⎟

⎜ R j 2 ⎟