Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 2

Министерство образования Российской Федерации

Санкт-Петербургский  государственный горный  институт им. Г.В. Плеханова

(технический университет)

Расчётно-графическое задание №2

По дисциплине:                       Сопротивление материалов

                                   (наименование учебной дисциплины согласно учебному плану)

Тема:           Построение эпюр поперечных сил, изгибающих моментов                                                                           и выбор сечений балок.

Выполнил: студент  гр. ТПР-01     ______________    /Самсоненко Е.В./

                                                                                                     ^{(подпись)                                  (Ф.И.О.)}  

ОЦЕНКА: _____________

Дата: __________________

ПРОВЕРИЛ:

Руководитель:           ____________            /Яковлев А.А./

                                                               ^{(подпись)                                         (Ф.И.О.)}

                                                            Санкт-Петербург

                                                                     2003

Вариант №18

Задание:

Построить эпюры поперечных сил, изгибающих моментов и подобрать сечения балок.

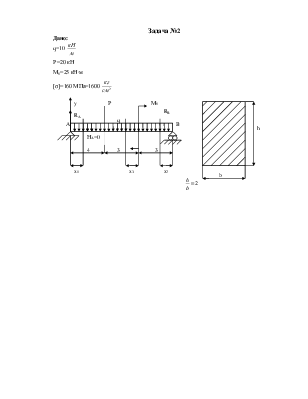
Задача №1

Дано:

q₁=5

q₂=10

М₀=25 кН∙м

[σ]=160 МПа=1600

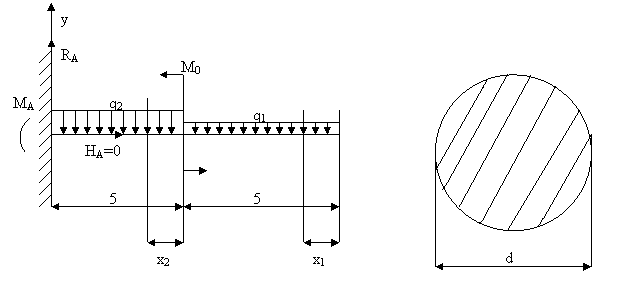
Поскольку опора представляет собой заделку, реакции этой опоры (R_A,M_A) можно не определять. Они получаются автоматически в процессе построения эпюр перерезывающих сил и изгибающих моментов.

Будем рассматривать сечения по длине балки – справа.

Участок №1 (справа):   0х₁5

Уравнение для Q(x₁):

Q(x₁)=q₁∙x₁ – уравнение наклонной прямой

х₁=0; Q(x₁)=0

х₁=5; Q(x₁)=q₁∙5=25 кН

Уравнение для М(x₁):

М(х₁)=-q₁∙ х₁∙ - уравнение параболы

х₁=0; М(х₁)=0

х₁=5; М(х₁)=-q₁∙5∙2,5=-62,5 кН∙м

Ветви параболы направлены вниз.

Участок №2 (справа):   0х₂5

Уравнение для Q(x₂):

Q(x₂)=q₁∙5+q₂∙x₂ – уравнение наклонной прямой

x₂=0; Q(x₂)= q₁∙5=25 кН

x₂=5; Q(x₂)=q₁∙5+q₂∙5=25+50=75 кН

Уравнение для М(x₂):

М(x₂)=-q₁∙ 5∙( x₂+2,5)+М₀-q₂∙ x₂ - уравнение параболы

x₂=0; М(x₂)=-q₁∙5∙2,5+М₀=-62,5+25=-37,5 кН∙м