Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 2, страница 2

x₂=5; М(x₂)=-q₁∙5∙7,5+М₀-q₂∙5∙2,5=-187,5+25-125=-287,5 кН∙м

Ветви параболы направлены вниз.

В точке приложения сосредоточенного момента М₀=25 кН∙м на эпюре Q(x) будет наблюдаться скачок, равный величине этого момента.

Проверка:

=0;   R_A-q₂∙5-q₁∙5=0;   R_A=q₂∙5+q₁∙5=25+50=75 кН

=0;   М_А-q₂∙5∙2,5+M₀-q₁∙5∙7,5=0;   M_A=q₂∙5∙2,5-M₀+q₁∙5∙7,5=287,5 кН∙м

Условие прочности:

σ_max=

-максимальный изгибающий момент с эпюры М(х)

=287,5 кН∙м=287,5∙10⁴ кг∙см

Момент сопротивления для круглого сечения: W=0,1d³

Из условия прочности:

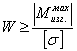;   откуда

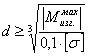=26 см0,26 м

Задача №2

Дано:

q=10

Р=20 кН

М₀=25 кН∙м

[σ]=160 МПа=1600

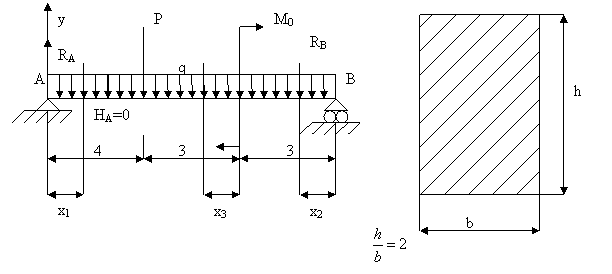
Определяем неизвестные реакции опор, составляя уравнения равновесия статики.

=0;   -q∙10∙5-P∙4-M₀+R_B∙10=0

-500-80-25+R_B∙10=0

R_B==60,5 кН

=0;   -R_A∙10+q∙10∙5+P∙6-M₀=0

-R_A∙10+500+120-25=0

R_A==59,5 кН

Проверка:

=0;   R_A-P-q∙10+R_B=0

59,5-100-20+60,5=0

              0=0

Реакции определены правильно.

Участок №1 (слева):   0х₁4

Уравнение для Q(x₁):

Q(x₁)=R_A-q∙x₁ – уравнение наклонной прямой

х₁=0; Q(x₁)=R_A=59,5 кН

х₁=4; Q(x₁)=R_A-q∙4=59,5-40=19,5 кН

Уравнение для М(x₁):

М(х₁)=R_A∙х₁-q∙х₁∙ - уравнение параболы

х₁=0; М(х₁)=0

х₁=4; М(х₁)=R_A∙4-q∙4∙2=238-80=158 кН∙м

Ветви параболы направлены вниз.

Участок №2 (справа):   0х₂3

Уравнение для Q(x₂):

Q(x₂)=-R_В+q∙x₂ – уравнение наклонной прямой

x₂=0; Q(x₂)=-R_В=-60,5 кН

x₂=3; Q(x₂)=-R_В+q∙3=-60,5+30=-30,5 кН

Уравнение для М(x₂):