Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 2, страница 7

Участок №2 (справа):   0х₂2

Уравнение для Q(x₂):

Q(x₂)=R_C – не зависит от x₂ – прямая, параллельная оси ОХ

x₂=0; Q(x₂)=R_C=1,4 кН

x₂=2; Q(x₂)=R_C=1,4 кН

Уравнение для М(x₂):

М(x₂)=М_С-R_C∙х₂ - уравнение наклонной прямой

x₂=0; М(x₂)=М_С=2,6 кН∙м

x₂=2; М(x₂)=М_С-R_C∙2=2,6-2,80 (шарнир “В” справа)

Участок №3 (справа):   0х₃2

Уравнение для Q(x₃):

Q(x₃)=R_C+P – не зависит от x₃ – прямая, параллельная оси ОХ

x₃=0; Q(x₃)=R_C+Р₁=1,4+20=21,4 кН

x₃=2; Q(x₃)=R_C+Р₁=1,4+20=21,4 кН

В точке приложения сосредоточенной силы Р=20кН на эпюре Q(х) будет наблюдаться скачок, равный величине этой реакции.

Уравнение для М(x₃):

М(x₃)=М_С-R_С∙(x₃+2)- Р∙x₃ - уравнение наклонной прямой

Для построения этой параболы найдём три её точки:

x₃=0; М(x₃)=М_С-R_С∙2=2,6-2,80 (шарнир “В” слева)

x₃=2; М(x₃)=М_С-R_С∙4-Р∙2=2,6-5,6-40=-43 кН∙м

В точке приложения сосредоточенного момента М₀=25кН на эпюре М(х) будет наблюдаться скачок, равный величине этого момента.

Условие прочности:

σ_max=

-максимальный изгибающий момент с эпюры М(х)

=43 кН∙м=43∙10⁴ кг∙см

Из условия прочности:

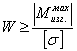=268 см³

Так как профиль состоит из двух швеллеров, то расчётное значение момента сопротивления уменьшаем вдвое: W_С=134 см³

По сортаменту прокатной стали, в соответствии с ГОСТ 8240-72 выбираем швеллеровый  профиль, у которого величина момента сопротивления близка к требуемой. Таких профилей два:

№20 с моментом сопротивления несколько большим, чем требуемый (W=152 см³)   

№18А с моментом сопротивления несколько меньшим, чем требуемый (W=132 см³)

Максимальные напряжения в швеллеровый  балке №20:

Недонапряжение:

Можно выбрать швеллер с моментом сопротивления меньшим, чем требуемый, при условии, если перенапряжение в нём не превышает

Максимальные напряжения в швеллеровый  балке №18А:

Перенапряжение:

, что допустимо.

Окончательно выбираем швеллер №18А.