В точке приложения сосредоточенной силы Р2=20 кН на эпюре Q(х) будет наблюдаться скачок, равный величине этой силы.
Эпюра Q(х3)
пересекает ось Х, меняя знак с плюса на минус. Найдём значение координаты ![]() , при котором Q(х3)=0
, при котором Q(х3)=0
Q(х3)=-Р1+RB-q∙![]() =0;
=0;
![]() =
=![]() =3,25 м
=3,25 м
Уравнение для М(x3):
М(x3)=Р1∙(x3+2)-RB∙x3+q∙х3![]() - уравнение параболы
- уравнение параболы
Для построения этой параболы найдём три её точки:
x3=0; М(x3)=Р1∙2=20 кН∙м
x3=4; М(x3)=Р1∙6-RB∙4+q∙4∙2=60-170+80=-30 кН∙м
Для нахождения третьей точки параболы воспользуемся дифференциальной зависимостью:
![]() =Q(x3)
=Q(x3)
Вычислим производную от М(x3), приравняем её к нулю и найдём значение
координаты ![]() , при котором изгибающий момент на
данном участке будет иметь экстремальное значение:
, при котором изгибающий момент на
данном участке будет иметь экстремальное значение:
![]() =Р1-RA+q∙
=Р1-RA+q∙![]() =0;
=0; ![]() =
=![]() =3,25 м
=3,25 м
Подставим значение координаты ![]() =3,25м в уравнение для М(х3)
и найдём экстремальное значение изгибающего момента на данном участке. В нашем
случае – минимум.
=3,25м в уравнение для М(х3)
и найдём экстремальное значение изгибающего момента на данном участке. В нашем
случае – минимум.
М(![]() )=Р1∙5,25-RВ∙3,25+q∙3,25∙1,625=52,5-138,125+52,812
)=Р1∙5,25-RВ∙3,25+q∙3,25∙1,625=52,5-138,125+52,812![]() -32,8 кН∙м
-32,8 кН∙м
Ветви параболы направлены вверх.
Условие прочности:
σmax=![]()
![]() -максимальный
изгибающий момент с эпюры М(х)
-максимальный
изгибающий момент с эпюры М(х)
![]() =37,8
кН∙м=37,8∙104 кг∙см
=37,8
кН∙м=37,8∙104 кг∙см
Из условия прочности:
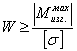 =
=![]() 236
см3
236
см3
По сортаменту прокатной стали, в соответствии с ГОСТ 8239-72 выбираем двутавровый профиль, у которого величина момента сопротивления близка к требуемой. Таких профилей два:
№22А с моментом сопротивления несколько большим, чем требуемый (W=254 см3)
№22 с моментом сопротивления несколько меньшим, чем требуемый (W=232 см3)
Максимальные напряжения в двутавровой балке №22А:
![]()
Недонапряжение:
![]()
Можно выбрать
двутавр с моментом сопротивления меньшим, чем требуемый, при условии, если
перенапряжение в нём не превышает ![]()
В нашем случае для двутавровой балки №22
![]()
Перенапряжение:
![]() , что допустимо.
, что допустимо.
Окончательно выбираем двутавр №22.
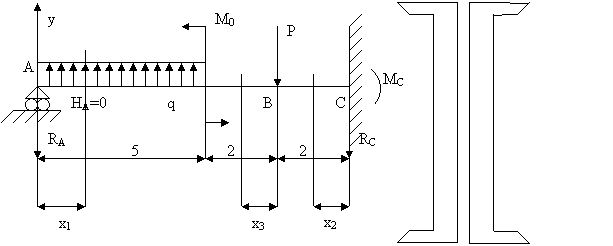
Задача №4
Дано:
q=10 ![]()
Р=20 кН
М0=25 кН∙м
[σ]=160 МПа=1600 ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.