Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 5

Министерство образования Российской Федерации

Санкт-Петербургский государственный горный институт

 (Технический Университет)

Кафедра механики

Расчетно–графическая работа №2

Дисциплина: Сопротивление материалов.

Вариант №3

Выполнил: ст. гр. ТО-01                             Подпись                                /Евдокименко Д.С./

Проверил:                                                     Подпись                                /Гореликов В.Г./

Санкт – Петербург

2003г.

Задача №1.

Дано:q₁=15 кН/м

q₂=20 кН/м

Эпюра Q(x).

Участок №1:                      0≤x₁≤3

    (слева)

Уравнение для Q(x₁):

 -уравнение наклонной прямой

x₁=0; Q(x₁)=0; x₁=3; Q(x₁)=q₂·3=60кН.

Участок №2:                      0≤x₂≤2

    (слева)

Уравнение для Q(x₂):

 -уравнение наклонной прямой

x₂=0; Q(x₂)= q₂·3=60 кН; x₂=2; Q(x₂)=q₂·3-q₁·2=30кН.

Участок №3:                      0≤x₃≤2

    (слева)

Уравнение для Q(x₃):

 -уравнение наклонной прямой

x₃=0; Q(x₃)= q₂·3-q₁·2=30 кН; x₃=2; Q(x₃)=q₂·3-q₁·2-+q₂·2=70кН.

Эпюра M(x)

Участок №1:                        0≤x₁≤3

    (слева)

Уравнение для M(x₁):

 -уравнение параболы

x₁=0; M(x₁)=0; x₁=3; М(x₁)=q₂·3·1.5=90кНм.

По правилу “зонтика” парабола выпуклостью вниз.

Участок №2:                        0≤x₂≤2

    (слева)

Уравнение для M(x₂):

 -уравнение парабола

x₂=0; M(x₂)= q₂·3·1,5=90 кНм; x₂=2; M(x₂)=q₂·3·3.5-q₁·2=180кНм.

По правилу “зонтика” парабола выпуклостью вверх.

Участок №3:                        0≤x₃≤2

    (слева)

Уравнение для M(x₃):

 -уравнение параболы

x₃=0; M(x₃)= q₂·3·3.5-q₁·2·1=180 кНм; x₃=2; M(x₃)=q₂·3·5.5-q₁·2·3+q₂·2·1=280кНм.

По правилу “зонтика” парабола выпуклостью вниз.

Проверка.

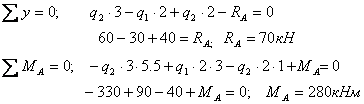
Условие прочности

Максимальный изгибающий момент с эпюры M(x)

=280кНм=280·10⁴кг·см

Момент сопротивления для круглого сечения: