Построение эпюр поперечных сил, изгибающих моментов и выбор сечений балок. Вариант № 5, страница 5

    (слева)

Уравнение для M(x₁):

 -уравнение наклонной прямой

x₁=0; M(x₁)=-М_о=-20кНм; x₁=2; М(x₁)=-М_о+R_A·2=0 (слева)

Участок №2:                        0≤x₂≤2

    (слева)

Уравнение для M(x₂):

 -уравнение параболы.

x₂=0; M(x₂)=-М_о+R_A·2=0(справа); x₂=2; M(x₂)=-М_о+R_A·4+P·2=-10кНм.

Участок №3:                        0≤x₃≤4

    (слева)

Уравнение для M(x₃):

 -уравнение параболы

x₃=0; M(x₃)= -M_o+R_A·4-P·2=-10 кНм; x₃=4; M(x₃)=-M_o+R_A·8-P·6-q·4·2=10кНм.

По правилу “зонтика” парабола выпуклостью вверх.

Условие прочности

Максимальный изгибающий момент с эпюры M(x)

=190кНм=190·10⁴кг·см

Из условия прочности:

,

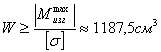так как профиль состоит из двух швеллеров, то расчетное значение момента сопротивления уменьшаем вдвое W≈594см³

По сортаменту прокатной стали ГОСТ 8240-56 выбираем швеллерный профиль, у которого величина момента сопротивления близка к требуемой. Таких профилей два: №36 с моментом сопротивления, несколько большим требуемого(W=601cм³) и №33 с моментом сопротивления несколько меньшим требуемого (W=484см³).

Максимальное напряжение в двутавровой балке №36

Недонапряжение

можно выбрать швеллер с моментом сопротивления меньшим, чем требуемый, при условии, если перенапряжение в нем не превышает 5%.

В нашем случае для двутавровой балки №33

Перенапряжение:

итак, принимаем швеллер №36