Из условия прочности:
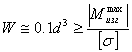 ,
откуда
,
откуда

Задача №2.
Дано:q=20 кН/м
Р=15 кН
Мо=20кНм
![]()
Определяем неизвестные реакции опор, составляя уравнения равновесия статики
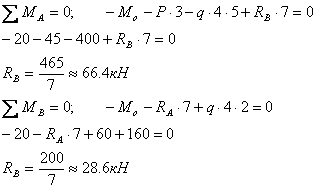
Проверка
![]()
Реакции опор определены правильно
Эпюра Q(x).
Участок №1: 0≤x1≤3
(слева)
Уравнение для Q(x1):
![]() -не зависит от x1
– прямая, параллельная оси x.
-не зависит от x1
– прямая, параллельная оси x.
x1=0; ![]() =28кН,6; x1=3;
=28кН,6; x1=3; ![]() =28кН.
=28кН.
Участок №2: 0≤x2≤4
(слева)
Уравнение для Q(x2):
![]() -уравнение
наклонной прямой
-уравнение
наклонной прямой
x2=0;
Q(x2)= -RB=-66.4 кН; x2=4;
![]() =13.6кН.
=13.6кН.
В точке приложения сосредоточенной силы Р=15кН, на эпюре Q(x) будет наблюдаться скачек, равный величине этой силы
Эпюра Q(x2) пересекает ось x, меняя знак с “-”на”+”
Найдем значение координаты x20, при котором Q(x2)=0
![]()
Эпюра M(x)
Участок №1: 0≤x1≤3
(слева)
Уравнение для M(x1):
![]() -уравнение
наклонной прямой
-уравнение
наклонной прямой
x1=0; M(x1)=Мо=20кНм; x1=3; М(x1)=Мо+RA·3=105.8кНм.
Участок №2: 0≤x2≤4
(слева)
Уравнение для M(x2):
![]() -уравнение
парабола
-уравнение
парабола
x2=0; M(x2)= 0; x2=4; M(x2)=RB·4-q2·2·4=105,8кНм.
Для отыскания третьей точки параболы воспользуемся дифференциальной зависимостью:
![]()
вычислим производную от М(x2), приравняем ее к нулю и найдем значение координаты x20, при котором изгибающий момент на данном участке будет иметь экстремальной значение
![]()
подставим значение координаты x20=3.32м в уравнение М(x2) и найдем экстремальное значение изгибающего момента на данном участке
![]()
По правилу “зонтика” парабола выпуклостью вверх.
Условие прочности
![]()
Максимальный изгибающий момент с эпюры M(x)
![]() =110,2кНм=110,2·104кг·см
=110,2кНм=110,2·104кг·см
Момент сопротивления для
прямоугольного сечения: ![]()
Из условия прочности:
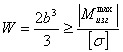 ,
откуда
,
откуда
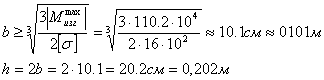
Задача №3.
Дано:q=20 кН/м
Р=15 кН
Мо=20кНм
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.