Федеральное агентство по образованию Российской Федерации
Санкт-Петербургский Государственный горный институт им. Г.В. Плеханова
(технический университет)

Кафедра механики
РГР №1
Расчет статически неопределимых стержневых систем
Вариант №40
Автор: студент гр.МЦ-О4 ____________ / ./
Оценка _____________
Дата ______________
Руководитель ____________ / Зарецкий-Феоктистов Г.Г./
Санкт-Петербург
2005
Задание. Рассчитать площади поперечных сечений стержней 1 и 2 исходя из расчета на прочность, при одновременном действии на конструкцию нагрузки Р, монтажных напряжений и температурных напряжений.
Рассчитываемая
система представляет собой стержневую конструкцию с одной шарнирной опорой и
двумя деформируемыми тягами (рис.1). Заданы материалы стержней: стержень 1 –
медь, стержень 2 – алюминий; модули их упругости при растяжении – сжатии: ![]() =
=![]() МПа;
МПа;
![]() МПа; внешние силы:
МПа; внешние силы: ![]() = 20 кH;
= 20 кH; ![]() = -20кН; q=-20
кН/м; коэффициенты линейного расширения материалов стержней
= -20кН; q=-20
кН/м; коэффициенты линейного расширения материалов стержней ![]() ,
, ![]() .
Неточность изготовления элемента системы: стержень 1 изготовлен длиннее на
величину
.
Неточность изготовления элемента системы: стержень 1 изготовлен длиннее на
величину ![]() м. Изменение температуры 2 стержня
м. Изменение температуры 2 стержня ![]() (охлаждение).
(охлаждение).
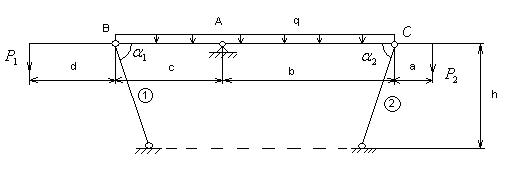
Рис.1
Допустимые
напряжения для материалов каждого из стержней: ![]() 100МПа,
100МПа,
![]() 80МПа. Конструктивное соотношение
площадей стержней
80МПа. Конструктивное соотношение
площадей стержней ![]() . Геометрические размеры
системы: a= 2м; b=3м; с=4м;d=1м; h=1м;
. Геометрические размеры
системы: a= 2м; b=3м; с=4м;d=1м; h=1м; ![]() =
=![]() ;
; ![]() =
=![]() .
.
Решение:
Вычертим расчетную схему балки с указанием всех размеров. Для расчета усилий используем метод сечений. Сечения проведем через оба стержня. Рассмотрим равновесие нижней части системы, заменяя действие отбрасываемой верхней части стержней внутренними усилиями (реакциями) R1, R2 (рис.2).
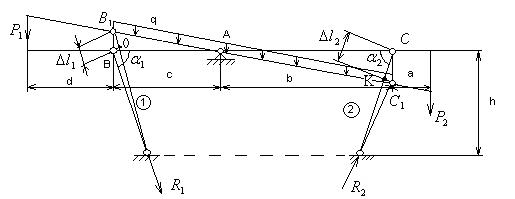
Рис.2
Cоставим уравнение статики:
![]()
или
![]() .
.
Остальные уравнения статики можно не составлять, так как они необходимы лишь при определении реакций в шарнире XA,YA, чего не требуется по условию задачи.
Таким образом, степень статической неопределимости системы К=1, так как мы имеем два неизвестных усилия R1, R2 и одно уравнение равновесия статики.
Для составления одного уравнения совместности деформаций необходимо рассмотреть схему перемещений системы (рис.2).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.