Расчет площади поперечных сечений стержней 1 и 2 исходя из расчета на прочность, при одновременном действии на конструкцию нагрузки Р, монтажных напряжений и температурных напряжений, страница 3

  (1);

2)Степень статической неопределимости системы  К=1.

3)Составим уравнение совместности деформации.

Из: (2);

Рассмотрим: ,

где  и    (3);

Из подобия     и   , с учетом (2) и (3)

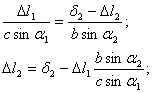
По закону Гука:

  и    уравнение (4) примет вид

,   т.к  и , то полученное выражение примет вид

 (5);

Уравнение (1) преобразуем

(6).

4)Решим систему  и уравнений (5) и (6):

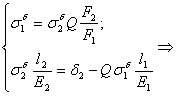
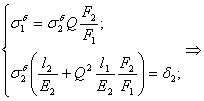
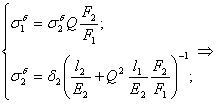
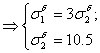
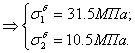
Т.к оба стержня сжимаются, то

ссчитаем температурные напряжения, т.е

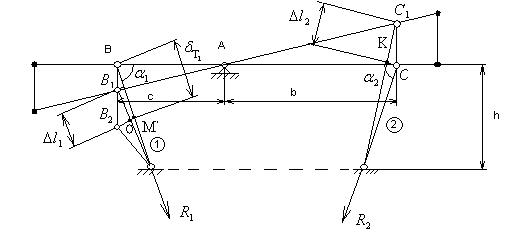
                                                                                                                             Рисунок4

1)Составим уравнение

 (1)

2) Степень статической неопределимости системы  К=1.

3) Составим уравнение совместности деформации.

Из : ;

     , : .

Рассмотрим  и . Они подобны

;

,

 (2)

По закону Гука:

  и    выражение (2) примет вид

(3).

Т.к  и ,то выражения (3) и (1) примут вид соответственно: