Расчет площади поперечных сечений стержней 1 и 2 исходя из расчета на прочность, при одновременном действии на конструкцию нагрузки Р, монтажных напряжений и температурных напряжений, страница 2

Под действием внешних сил Р₁ и Р₂ первый стержень удлинится на величину , а второй – на величину , при этом жесткая балка BC повернется в положение B₁C₁. Ввиду малости упругих деформаций горизонтальными смещениями точек B и C  в ходе деформирования системы переместится строго вертикально и займут положение В₁ и С₁. Удлинения и  находим также графически.

Рассмотрим :       (2);       

                      :        (3).

Рассмотрим  и . Они подобны

  (4)                  

Подставив равенства (2) и (3) в формулу (4), получим условие совместности деформаций для заданной стержневой системы:

;

, обозначим  - безразмерный коэффициент, учитывающий особенности геометрической конфигурации системы, тогда

               (5).

 По закону Гука  ,  (5) примет вид

;

Пусть ,тогда

   (6).

Решим систему из уравнений (1) и (6)

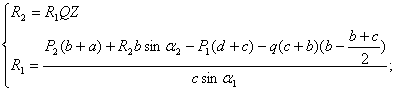
Вычислим   Q и Z:

 ,  и   из  рис.1       и  ;

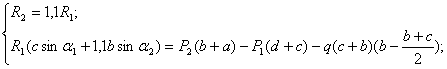
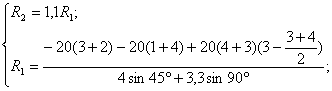
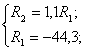
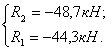
Т.к.  первый стержень растягивается, то напряжения в нем считаются положительными.

Значит: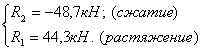

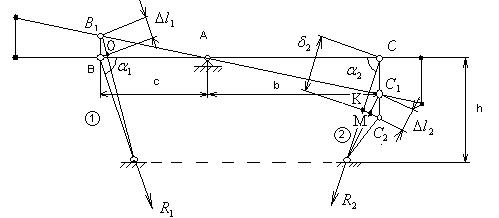
2. Определение напряжений, вызванных неточностью изготовления (P=0, .

                                                                                                    Рисунок 3

Составим уравнение равновесия .

;