Структурный, динамический и силовой анализ рычажного механизма. Проектирование кинематической схемы планетарного редуктора. Синтез кулачкового механизма

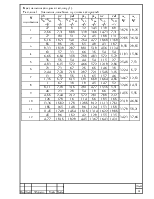
ИСХОДНЫЕ ДАННЫЕ

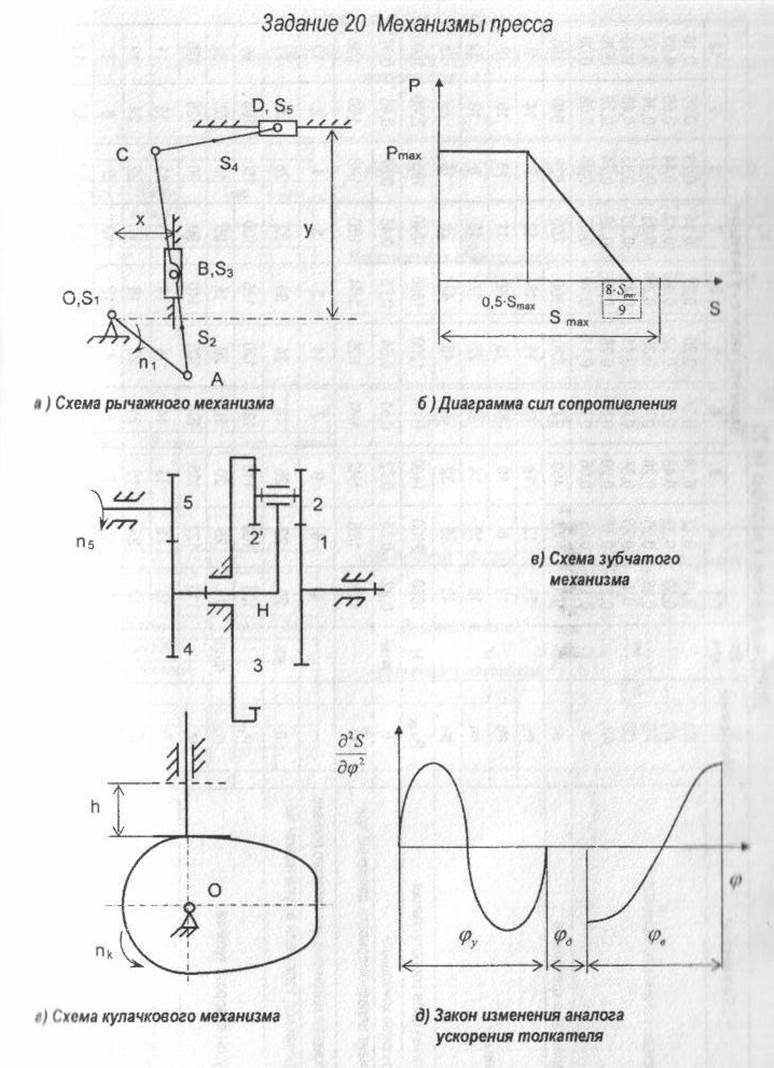
Рисунок 1–Исходные данные

1 СТРУКТУРНЫЙ АНАЛИЗ МЕХАНИЗМОВ

1.1 Структурный анализ рычажного механизма

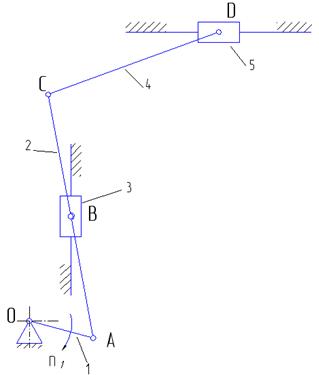
Подвижные звенья механизма.

1-кривошип

2-коромысло

3-ползун

4-шатун

5-ползун

Кинематические пары.

О (0-1),вр.,5 кл.

А (1-2),вр.,5 кл.

В (2-3),вр.,5 кл.

B` (0-3),пост.,5 кл.

С (2-4),вр.,5 кл.

D (4-5),вр.,5 кл.

D` (0-5),пост.,5 кл.                            

Найдём число степеней свободы.

Запишем формулу Чебышева.  Рисунок 2

W=3∙n-2∙P₅-P₄                                               (1.1)

Где,W-число степеней свободы,

n-число подвижных звеньев,

P₄-число пар 4-го класса,

P₅-число пар 5-го класса.

W=3∙5-2∙7=1

Число степеней свободы рычажного механизма равно 1.

Разобьём механизм на группы Ассура и

рассмотрим каждую группу в отдельности.

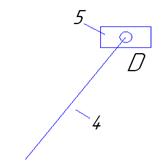
Группа 4-5 (Рисунок 6)

D` (0-5)-внешняя

C (3-4)-внешняя

D (4-5)-внутренняя

W=3∙2-2∙3=0                                                             

Рисунок 3- Группа (4-5)

IIкл.2 вид

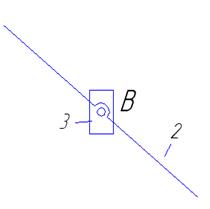Группа 2-3 (Рисунок 4)

А (1-3)-внешняя

В (2-3)-внутренняя

B` (0-3)-внешняя

W=3∙2-2∙3=0        

IIкл. 2 вид

Рисунок 4– Группа (2-3)

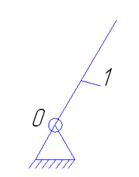
Начальное звено (Рисунок 8)                               

O (0-1)

W=3-2=1

Рисунок 5 – Начальный механизм

Составим структурную формулу: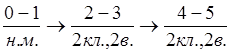

Вывод: весь механизм 2кл., 2вид

2. ДИНАМИЧЕСКИЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

2.1 Определение скоростей

Для заданной схемы механизма строим 12 положений.

Определяем масштабный коэффициент построения механизма:

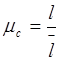                                                            (2.1)

где, - масштабный коэффициент,

 - длина звена,

 - длина звена на чертеже, 

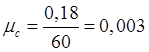
Запишем длинны звеньев механизма на чертеже

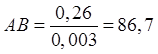
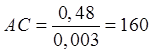
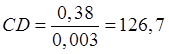
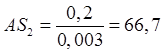
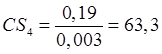
Приступаем к построению повёрнутых планов скоростей для каждого положения. Рассмотрим пример построения для положения №9:

У кривошипа определяем скорость точки А

                                             (2.2)

где,- длина звена,

 - угловая скорость кривошипа,

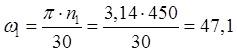
Для построения вектора скорости точки А определяем масштабный коэффициент

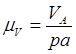                                                (2.3)

где, - скорость точки А,

 - вектор скорости точки А,

 - полюс, выбираемый произвольно

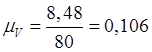
Для определения скорости точки B запишем  систему уравнений:

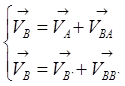                                       (2.4)

Вектор скорости точки А – V_A известен по величине и по направлению.  Известна линия действия вектора скорости точки B – V<sub>BB`.</sub>ТочкаB` лежит на неподвижной направляющей, по которой движется ползун(). Линия действия V_BB` направлена вдоль неподвижной направляющей.

Вектор скорости V_BA  не известен ни по величине, ни по направлению, но нам известна его линиядействия, она перпендикулярна  звену AB (на повернутом плане скоростей она будет параллельна звену AB), и проходит через точку a. На пересечении линии действия V_BAс линией действия вектора скорости V_BB` получим точку b. Соединив, полученную точку с полюсом p найдём длину вектора скорости точки B.

Так как центр массы 3-го звена совпадает точкой B то,

Для определения скорости центра масс 2-го звена S₂ воспользуемся соотношением:

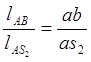                                             (2.5)

где,, - расстояния между соответствующими точками на механизме, м

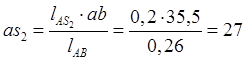,  - длинны векторов скоростей на плане, мм

 мм

Соединив, точку  и p получим скорость центра масс второго звена.

Запишем систему уравнений для определения скорости точки C:

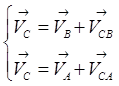
Линия действия векторов V_CAи V_CBизвестна. На повернутом плане скоростей она проходит параллельно звену AC.Вектор скорости V_CA  равен сумме векторов  V_ABиV_BС.Вектор скоростиV_BCпо величине и направлениюпропорционально равен вектору скорости V_AB, исходя из того, что точки A,B,C находятся на одном звене. Отложив из точки b вектор V_BC, получим точку c. Соединивполученную точку с полюсом p найдём длину вектора скорости точки  C.

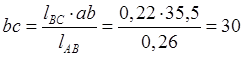 мм

Для определения скорости точки D запишем следующую систему уравнений: 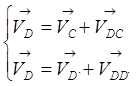                                                                                                                                                                     (2.6)

Вектор скорости точки С– V_С известен по величине и по направлению.  Известна линия действия вектора скорости точки D – V<sub>DD`.</sub> Точка D` лежит на неподвижной направляющей, по которой движется ползун(). Линия действия V_{DD`</sub> направлена вдоль неподвижной направляющей. Вектор скорости V<sub>DC</sub>  не известен ни по величине, ни по направлению, но нам известна его линия действия, она перпендикулярна  звену CD (на повернутом плане скоростей она будет параллельна звену CD), и проходит через точку c. На пересечении линии действия V<sub>DC</sub> с линией действия вектора скорости  V<sub>DD`} получим точку d. Соединив, полученную точку с полюсом p найдём длину вектора скорости точки D.

Для определения скорости центра масс 4-го звена S₄ воспользуемся соотношением:

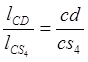                                             (2.7)

где,, - расстояния между соответствующими точками на механизме, м

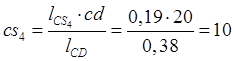,  - длинны векторов скоростей на плане, мм

 мм

Так как центр массы 5-го звена совпадает точкой D то,

                              (2.8)

Определим значения угловых скоростей звеньев.

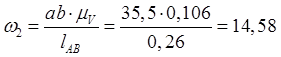
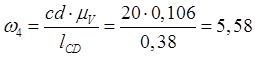
Скорости точек остальных положений определяются аналогичным образом.

Все значения сводим в таблицу(1).

Таблица 1 – Значения линейных и угловых скоростей