Структурный, динамический и силовой анализ рычажного механизма. Проектирование кинематической схемы планетарного редуктора. Синтез кулачкового механизма, страница 7

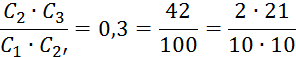
Из условия соосности

Тогда          

Для того, чтобы  принимаем .

Имеем

Проверим передаточное отношение

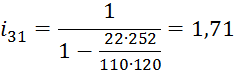
Определим количество сателлитов из условия соседства:

, где k – число сателлитов.

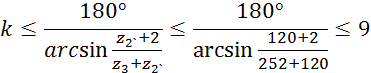
Проверим условие сборки:

,                                

где С – любое целое число.

Принимаем число сателлитов k=2.

Тогда

Условие сборки выполняется.

Для построения схемы зубчатого механизма определим делительные диаметры колес:

где  диаметр i-го колеса, мм.

Тогда

Масштабный коэффициент построения редуктора:

, где        - масштабный коэффициент построения редуктора;

 - принятое значение делительного диаметра колеса 3 на чертеже, мм.

4.2 Расчет параметров зубчатого зацепления 4-5

Найдем коэффициент смещения для колеса, у которого

, где X – коэффициент смещения зубчатого колеса, мм,

Z – число зубьев колеса.

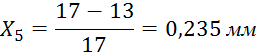
Суммарный коэффициент зацепления:

Зацепление положительное.

Определяем инвалюту угла зацепления:

, где  - инвалюта угла зацепления;       

 - значение инвалюты для стандартного угла зацепления

();

 - стандартный угол зацепления ().

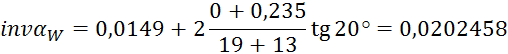
По инвалюте определяем угол зацепления:

Радиусы основных окружностей:

, где  - радиус основной окружности колеса, мм;

 - радиус делительной окружности колеса, мм.

Радиусы начальных окружностей:

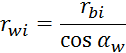
где  - радиус начальной окружности колеса, мм;

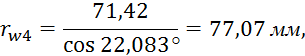
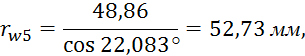
Межосевое расстояние:

, где  - межосевое расстояние, мм.

Радиусы окружностей вершин:

где  - радиус окружности вершин колеса, мм.

Радиусы окружностей впадин:

где  - радиус окружности впадин колеса, мм.

Радиус переходной поверхности ножки зуба:

Шаг зацепления по делительной окружности, мм:

Высота зуба, мм:

Толщины зубьев по делительной окружности  и :

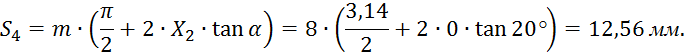
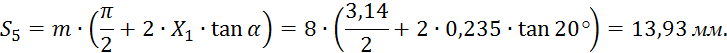
Углы профиля зуба по окружности вершин:

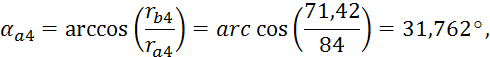
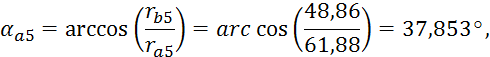
где  - углы профилей четвёртого и пятого зубчатых колес, град.

064677

Толщина зубьев по окружности вершин:

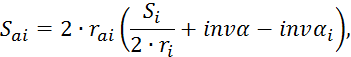
где  - толщины зубьев первого и второго колеса по окружности вершин, мм.

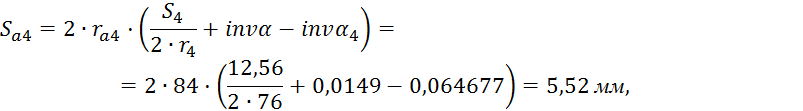
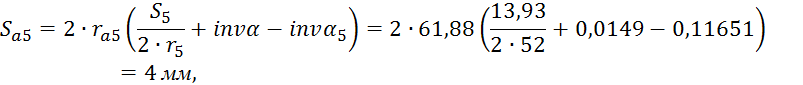
Проверим колеса на отсутствие заострения:

  Толщины зубьев по окружности вершин превышают минимально допустимое значение следовательно, заострение отсутствует.

Коэффициент зацепления зубчатой передачи:

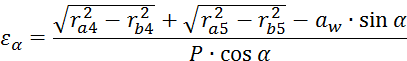
Подставляем численные значения и получаем:

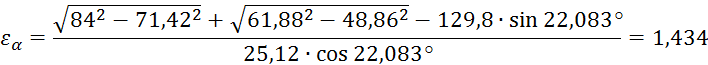
Радиус кривизны эвольвенты на вершине зуба :

Угловой шаг зубьев:

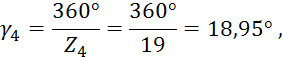
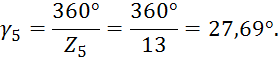
где  - угловой шаг зубьев колес 4 и 5.

Масштабный коэффициент построения эвольвентного зацепления:

.

где  - высота зуба на чертеже, мм.

Сведем все параметры в таблицу 11.

Таблица 11 – Параметры зацепления

r	76	52	71,42	48,86	77,07	52,73	84	61,88	66	43,88	5,52	4	18
	316,7	216,7	297,6	203,6	321,1	219,7	350	257,8	275	182,8	23	16,7	75

Определим графически коэффициент зацепления:

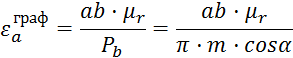
где         отрезок снятый с чертежа зацепления;

шаг колес по основной окружности;

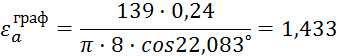
Определим погрешность определения:

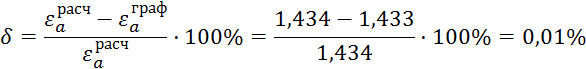
где          погрешность определения

5. СИНТЕЗ КУЛАЧКОВОГО МЕХАНИЗМА

5.1 Построение графиков аналогов скоростей, ускорений и пути

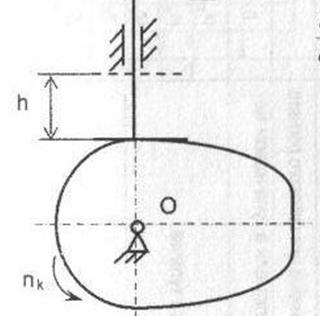
Рисунок 11 Схема кулачкового механизма

1-  Кулачок; 2-тарелка; 3-Толкатель;

Рабочая фаза кулачка

где         фаза удаления;

фаза дальнего стояния;

фаза возврата;

Примем отрезок  тогда масштабный коэффициент по оси :

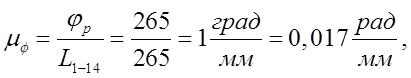
где         длина рабочей фазы кулачка на графике, мм.

Отрезки  и  при графическом интегрировании принимаем равными 40мм.

Построение ведем в следующей последовательности:

- Методом графического интегрирования (в  произвольном масштабе) диаграммы  получаем диаграмму  скоростей  толкателя . Эта же диаграмма одновременно является диаграммой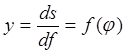

- Методом  графического  интегрирования диаграммы скоростей получаем диаграмму линейных перемещения толкателя или .