Структурный, динамический и силовой анализ рычажного механизма. Проектирование кинематической схемы планетарного редуктора. Синтез кулачкового механизма, страница 3

g – ускорение свободного падения, м/с² (g=9,8 м/с²).

G₂= 18·9,8=176H

G₃=10·9,8=98H

G₄=14·9,8=137Н

G₅=32·9,8=314 Н

2.4 Определение приведенной силы P_пр

Приведенную силу будем определять по методу Жуковского. Составим уравнения моментов всех сил относительно полюса р для каждого положения. pa, pс, pd, h₂, h₄– плечи сил (снимаются с плана скоростей), мм.

Направление приведенной силы для двигателей (наш случай) направлено в сторону угловой скорости кривошипа ω₁.

Для положения 1:

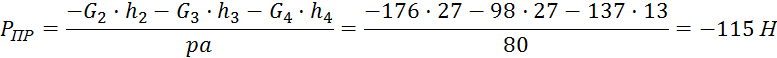
Для положения 2:

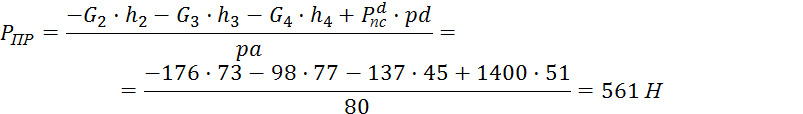
Для положения 3:

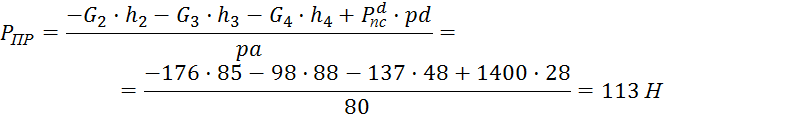
Для положения 4:

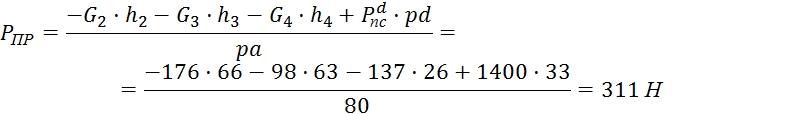
Для положения 5:

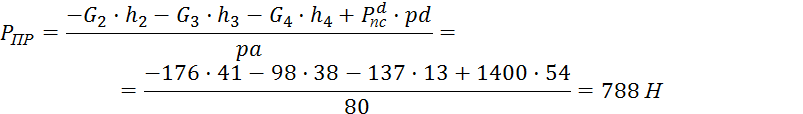
Для положения 6:

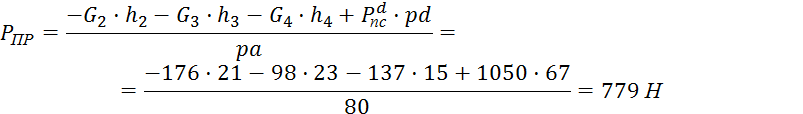
Для положения 7:

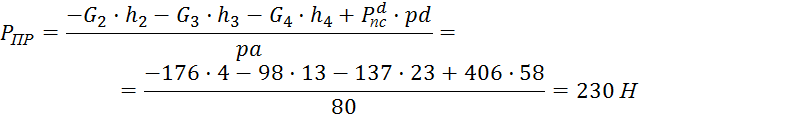
Для положения 8:

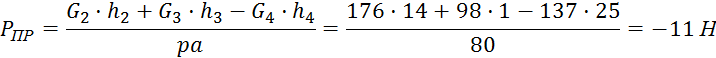
Для положения 9:

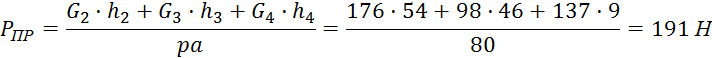
Для положения 10:

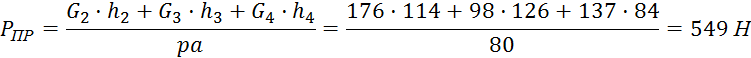
Для положения 11:

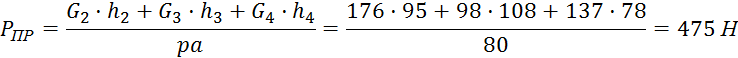
Для положения 12:

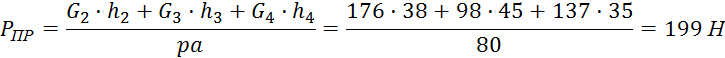
2.5 Определение приведенного момента сил сопротивления М_C

Приведенный момент будем определять по формуле:

M_C=P_ПР·l_OA, где     М_С – приведенный момент сопротивления, Н·м.

Для расчетного положения9

М_С=191·0,18=34,4 Н·м, остальные результаты расчетов сносим в таблицу 3.

Таблица 3 – Приведенная сила и момент сопротивления

	1	2	3	4	5	6	7	8	9	10	11	12
РПР,Н	-115	561	113	311	788	779	23	-11	191	549	475	199
МС,Н·м	-20,7	101	20,3	56	141,8	140,2	4,1	-2,0	34,4	98,8	85,5	35,8
L, мм	15	71	14	39	100	99	3	1	24	70	60	25

Масштабный коэффициент М_С(φ) по оси φ:

μ_φ=360/L_1-1=2·π/180=0,035

где     μ_φ – масштабный коэффициент по оси угла поворота, ;

L_1-1 – отрезок изображающий один оборот кривошипа, мм (принимаем 180 мм).

Масштабный коэффициент по оси моментов:

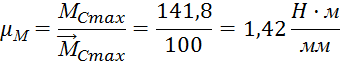
где      – значение максимального момента сопротивления, Н·м;

 – значение максимального момента сопротивления на графике, мм (принимаем 100 мм).

Строим график моментов. Значение момента на графике:

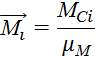
Полученные величины занесем в таблицу 5.

2.6 Построение графиков работ сил сопротивления и изменения кинетической энергии

График работ сил сопротивления строим графическим интегрированием графика М_дв(φ).

Масштабный коэффициент:

μ_А=μ_М·μ_φ·p₁, где μ_А – масштабный коэффициент по оси работ графика А(φ), ;

p₁ – расстояние от полюса до начала координат, мм, (прин. р=40 мм).

μ_А=1,42·0,035·40=1,99.

График изменения работы движущих сил А_д получаем, соединив начало и конец кривой А_с. Продифференцировав А_д на график моментов, получаем график моментов движущих сил М_дв.

Движущий момент М_дв:

М_дв=(1-m)·μ_М=40,5·1,42=57,5 Н·м, где         (1-m)–величина отрезка, снимаемая с графика, мм.

График изменения кинетической энергии строим в масштабе μ_Т:

μ_А=μ_Т=1,99.

Изменение кинетической энергии ΔТ определяется по формуле

ΔТ=А_д-А_с

для каждого из 12 положений. Откладываем для соответствующего положения.

2.7 Определение приведенного момента инерции

Приведенный момент инерции:

,

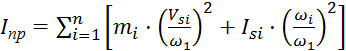где         m_i – масса i-го звена рычажного механизма, кг;

V_si – скорость центра масс i-го звена, м/с;

ω_i – угловая скорость i-го звена, с^-1;

I_si – приведенный момент инерции i-го звена по отношению к центру масс, кг·м².

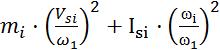–для звена, совершающего сложное движение;

 - для звена, совершающего вращательное или колебательное движения;

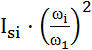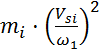 - для звена, совершающего поступательное движение.

Приведенный момент инерцииI_пр для нашегомеханизма определяем по формуле

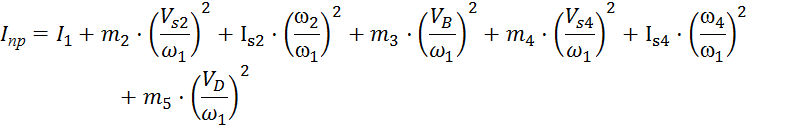
где I_S2,I_S4 – моменты инерции 2-го и 4-го звена относительно центра тяжести, кг·м².

Приведенные моменты инерции для звеньев определим по формуле:

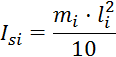
ОпределяемI_S2, I_S4 :

:

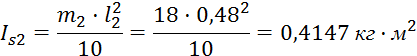
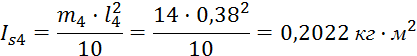
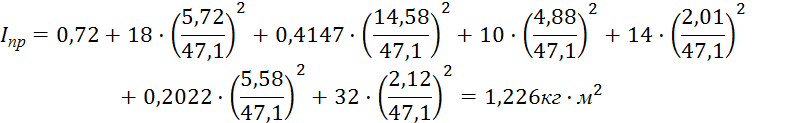
Расчет приведенного момента инерции для 12 положений сводим в таблицу 4

Таблица 4 – Момент инерции для 12 положений, кг·м²