Структурный, динамический и силовой анализ рычажного механизма. Проектирование кинематической схемы планетарного редуктора. Синтез кулачкового механизма, страница 4

								Iпр
1	0,72	0,093	0,176	0,037	0,085	0,034	0,000	1,144
2		0,499	0,091	0,300	0,144	0,122	0,422	2,298
3		0,659	0,017	0,392	0,170	0,081	0,127	2,166
4		0,398	0,027	0,201	0,102	0,021	0,177	1,645
5		0,176	0,121	0,073	0,206	0,005	0,472	1,774
6		0,072	0,194	0,027	0,328	0,006	0,727	2,074
7		0,030	0,225	0,009	0,300	0,015	0,546	1,843
8		0,033	0,197	0,000	0,144	0,019	0,146	1,258
9		0,265	0,040	0,107	0,025	0,003	0,065	1,226
10		1,184	0,101	0,805	0,525	0,200	0,042	3,576
11		0,841	0,213	0,591	1,090	0,230	3,177	6,861
12		0,161	0,219	0,103	1,179	0,129	5,368	7,878

Масштабный коэффициент по оси φ не изменяем.

Масштабный коэффициент по оси моментов:

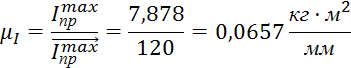
где     μ_I – масштабный коэффициент по оси приведенных моментов инерции;

 – значение максимального приведенного момента инерции, кг·м²;

 – значение максимального момента сопротивления на графике, мм.

Строим график приведенных моментов инерции. Значение приведенного момента инерции на графике сносим в таблицу 5.

Таблица 5 – Приведенный момент инерции и его значение на графике

	1	2	3	4	5	6	7	8	9	10	11	12
Iпр, кг·м2	1,144	2,298	2,166	1,645	1,774	2,074	1,843	1,258	1,226	3,576	6,861	7,878
, мм	17	35	33	25	27	32	28	19	19	54	105	120

2.8 Определение параметров маховика

Строим диаграмму энергия-масса (петля Виттенбауера) на основе графика приведенного момента инерции и графика изменения кинетической энергии, графически исключая ось φ.

К полученной кривой энергия-масса под углами ψ_minи ψ_maxпроводим касательные.

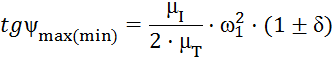
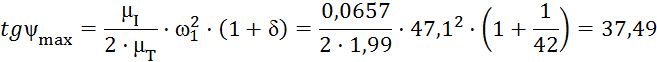
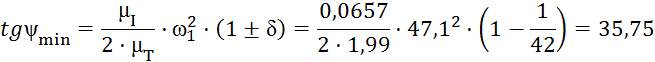
где         ψ_minи ψ_max – углы наклона касательных проведенных к петле Виттенбауера, град;

δ – коэффициент неравномерности вращения кривошипа.

Получаем значения углов ψ_max=88,47˚;  ψ_min=88,40˚.

Определяем отрезок aс, который отсекают касательные по оси ΔТ. Так как он полностью не попадает в область графика, находим его длину через отрезок bd.

aс=od·tgψ_min-ob·tgψ_max=123·35,75-15·37,49=3835мм

Приведенный момент инерции маховика I_M:

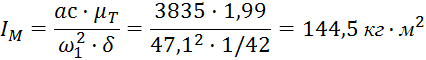
Определяем диаметр маховика:

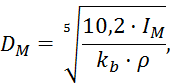
где         D_M – диаметр маховика, м;

ρ – плотность материала маховика, (сталь,ρ=7800 кг/м³);

k_b – коэффициент соотношения диаметра и ширины маховика (принимаем k_b=0,15).

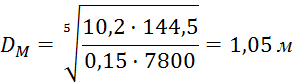
Определяем ширину маховика b:

b=k_b·D_M=0,15·1,05=0,16 м

Определяем массу маховика m_М:

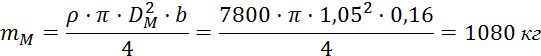
где         m_M – масса маховика, кг.

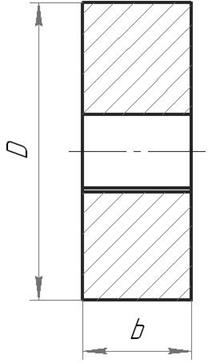
Рисунок 6 - Эскиз маховика

3. СИЛОВОЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

3.1 Построение плана ускорений

Проводим силовой анализ для положения 9 на рабочем ходу.

Ускорение точки О равно нулю (а_о=0).

Для определения ускорений точекА и С(а_А=а_С) разложим ускорение точкиА на нормальную и тангенциальную составляющие:

где          - полное ускорение точки А, м/с²;

 - нормальное ускорение точкиА, м/с²;