Структурный, динамический и силовой анализ рычажного механизма. Проектирование кинематической схемы планетарного редуктора. Синтез кулачкового механизма, страница 6

 - вектор силы  на плане сил, мм.

Значение векторов сил для звена 5 поместим в таблицу 7.

Таблица 7 – Значение сил и их векторов на плане сил

Силы
Рi, Н	314	4576	732
, мм	14	200	32

Величина неизвестной реакции:

Определим точку приложения реакции  . Составим уравнение моментов сил звена 5 относительно точки S₄    .

где h – плечо силы R₅₀относительно точки s₄.

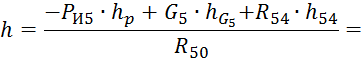
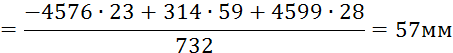
Рассмотрим группу 2-3

Составим векторное уравнение сил:

Найдем реакцию  .

, где         R^τ₂₁ – касательная составляющая реакции 1-го звена на звено 2;

h_РИ2, h_G2, AС – плечи сил снятые с чертежа, мм.

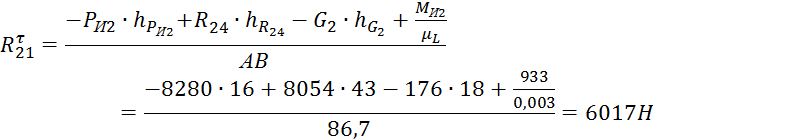
Rⁿ₂₁и R₃₀ определим графически из плана сил.

Определим масштабный коэффициент для группы 2-3:

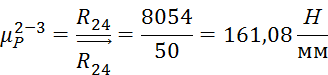
где          - масштабный коэффициент плана сил группы 2-3, ;

 - вектор силы  на плане сил, мм.

Значение векторов сил для группы 3-2 поместим в таблицу 8.

Таблица 8 – Значение сил и их векторов на плане сил

Силы
Рi, Н	8280	176	6080	98	6017	8054
, мм	52	1	38	1	37	50

Последовательно по векторному уравнению откладываем вектора сил. Неизвестные реакции определим графически:

Для нахождения  составим уравнение сил для 3-го звена

Масштабный коэффициент плана сил 3-го звена:

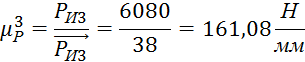
где          - масштабный коэффициент плана сил звена 3, ;

 - вектор силы  на плане сил, мм.

Значение векторов сил для звена 3 поместим в таблицу 9.

Таблица 9 – Значение сил и их векторов на плане сил

Силы
Рi, Н	98	6080	56539
, мм	1	38	351

Величина неизвестной реакции:

Определим точку приложения реакции  . Составим уравнение моментов сил звена 3 относительно точки S₂    .

где h – плечо силы R₃₀относительно точки s₂.

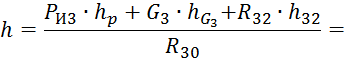
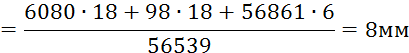
Рассмотрим начальный механизм 0-1

Составим уравнение моментов, из которого определим уравновешивающую силу

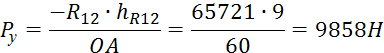
Реакцию R₁₀определим графически из условия

Масштабный коэффициент плана сил начального механизма:

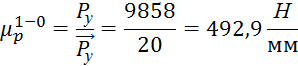
где  - вектор силы R₁₂на плане сил, мм.

Строим план сил и определяем неизвестную реакцию

Определяем уравновешивающий момент М_У по формуле:

3.5 Определение уравновешивающей силы по методу Жуковского.

Заменим моменты инерции, действующие на звенья, парами сил

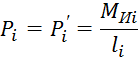
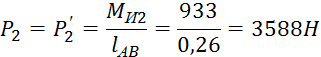
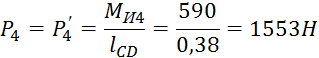
Вычерчиваем повернутый на 90˚ план скоростей и прикладываем к нему все действующие на механизм силы, сохраняя их направления. Составим уравнение равновесия для всех сил относительно полюса

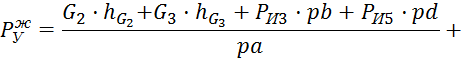
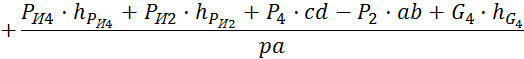
где         pa, ps₂, h_G2, h_Pи2, pb, ps₄, pd, h_Pи4, h_G4– плечисил, мм.

P_у^ж– уравновешивающая сила, определенная по методу Жуковского, Н

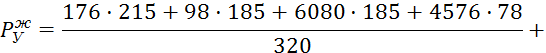
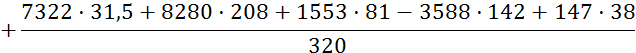
Уравновешивающий момент M_у^ж

Погрешность двух методов составляет:

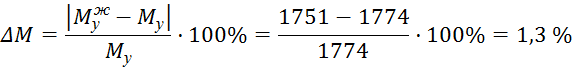
4. ПРОЕКТИРОВАНИЕ КИНЕМАТИЧЕСКОЙ СХЕМЫ ПЛАНЕТАРНОГО РЕДУКТОРА. РАСЧЕТ ЭВОЛЬВЕНТНОГО ЗАЦЕПЛЕНИЯ

4.1 Расчет планетарного редуктора

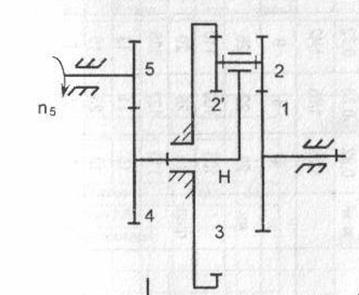
Рисунок 7 – Схема передаточного зубчатого механизма

1-Опорное центральное колесо, 2-2` -Блок сателлитов; 3- Центральное опорное колесо; 4,5-Зубчатые колёса рядовой передачи;

Для проектирования передаточного зубчатого механизма нам заданы следующие параметры: модуль зацепления m=8 мм число зубьев колес Z₄=19, Z₅=13, передаточное отношение механизма .

Передаточное отношение механизма:

где  - передаточное отношение планетарной передачи;

 - передаточное отношение рядовой передачи;

,

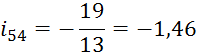
Знак минуса передаточного отношения показывает, что колёса 4 и 5 вращаются в разные стороны.

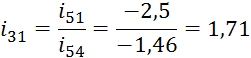
Для определения  через числа зубьев планетарного механизма используем выражение:

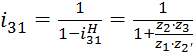, где  – числа зубьев колес планетарной передачи.

Условие соосности:

,

Исходя из выше изложенного, находим соотношение чисел зубьев:

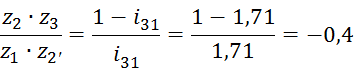
Заменяем

где a,b – коэффициенты, на которые домножим для выполнения условий.