Структурный, динамический и силовой анализ рычажного механизма. Проектирование кинематической схемы планетарного редуктора. Синтез кулачкового механизма, страница 5

 – тангенциальное ускорение точкиА, м/с².

Тангенциальное ускорение точкиА=0, т.к. угловое ускорение кривошипа ОА ε₁=0.

Тогда  . Нормальное ускорение точкиА:

Масштабный коэффициент плана ускорений:

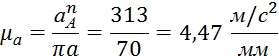
где         μ_а – масштабный коэффициент плана ускорений;

a – вектор ускорений точки А, мм.

Ускорение точки B:

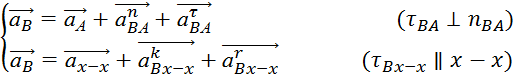
где  - ускорение точки B, м/с²;

 - нормальное ускорение точки B относительно точки A, м/с²;

 - тангенциальное ускорение точкиBотносительно точки A, м/с²;

 - кориолисово ускорение точки B при движении по направляющей Х-Х, м/с²;

 - относительное ускорение точки B при движении по направляющей Х-Х, м/с²;

 - ускорение направляющей Х-Х, м/с².

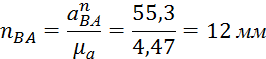
Так как направляющая Х-Х неподвижна,  и . Откладываем  от конца вектора а_А (точка а), из полученной точки – прямую параллельную . Проводим прямую параллельную  из полюса. Пересечение прямых даст конец вектора а_B – точка B.

Для определения ускорения  центра масс 2-го звена S₂ воспользуемся соотношением:

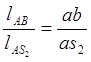                                                 (2.5)

где, , - расстояния между соответствующими точками на механизме, м

,  - длинны векторов ускорений на плане, мм

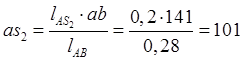 мм

Ускорение точки С найдём из соотношения:

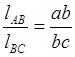
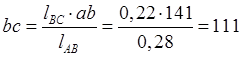 мм

Ускорение точки D:

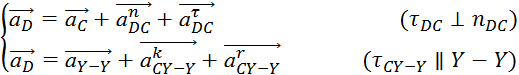
где  - ускорение точки D, м/с²;

 - нормальное ускорение точки Dотносительно точки C, м/с²;

 - тангенциальное ускорение точки Dотносительно точки C, м/с²;

 - кориолисово ускорение точки D при движении по направляющей Y-Y, м/с²;

 - относительное ускорение точки D при движении по направляющей Y-Y, м/с²;

 - ускорение направляющей Y-Y, м/с².

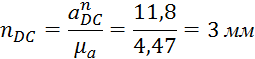
Так как направляющая Y-Y неподвижна,  и . Откладываем  от конца вектора а_C (точка C), из полученной точки – прямую параллельную . Проводим прямую параллельную  из полюса. Пересечение прямых даст конец вектора а_D – точка d.

Определяем положение точек  S₃, S₄, S₅. Положение векторов  ускорений точек S₃, S₅ совпадают с положением векторов точек B и D соответственно.

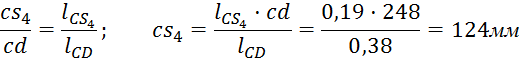
где - отрезок на плане ускорений, мм.

3.2 Определение значений ускорений

Величину неизвестных линейных ускорений определяем используя построенный план ускорений.

где         а_i – ускорение точки или звена, м/с²;

- вектор ускорения точки или звена (снимается с плана ускорений), мм.

Определим угловые ускорения звеньев:

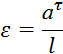
где         ε – угловое ускорение звена, с^-2;

а^τ  - тангенциальное ускорение звена, м/с²;

l – длина звена, м.

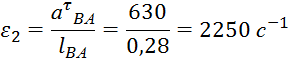
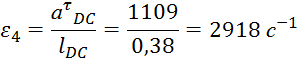
4.3 Определение сил инерции и моментов инерции

Определим силы инерции:

Р_И=m·a_S, где         Р_И – приведенная сила инерции, Н;

m – масса звена, кг;

а_S – ускорение центра масс звена, м/с².

Р_И2=m₂·а_S2=18·460=8280Н;

Р_И4=m₄·а_S4=14·523=7322Н;

Р_И3=m₃·а_В=10·608=6080Н;

Р_И5=m₅·а_d=32·143=4576Н;

Рассчитываем моменты инерции:

М_И=I_S·ε_i, где         М_И – приведенный момент инерции, Н·м;

I_S – приведенный момент инерции звена по отношению к центру масс, кг·м²;

М_И2=0,4147·2250=933 Н·м;

М_И4=0,2022·2918=590 Н·м;

4.4 Силовой расчет методом планов сил

Рассмотрим группу 4-5

Составим векторное уравнение сил:

Найдем реакцию  .

, где         R^τ₄₂ – касательная составляющая реакции 4-го звена на звено 2;

h_РИ4, h_G4, СD– плечи сил снятые с чертежа, мм.

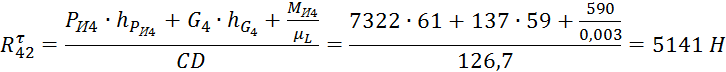
Rⁿ₄₂ и R₅₀ определим графически из плана сил.

Определим масштабный коэффициент для группы 4-5:

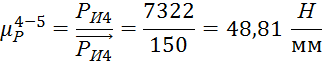
где          - масштабный коэффициент плана сил группы 4-5, ;

 - вектор силы  на плане сил, мм.

Значение векторов сил для группы 5-4 поместим в таблицу 6.

Таблица 6 – Значение сил и их векторов на плане сил

Силы
Рi, Н	7322	147	4576	314	5141
, мм	150	3	94	6	105

Последовательно по векторному уравнению откладываем вектора сил. Неизвестные реакции определим графически:

Для нахождения  составим уравнение сил для 5-го звена

Масштабный коэффициент плана сил 5-го звена:

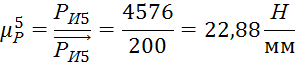
где          - масштабный коэффициент плана сил звена 5, ;