Проведение своеобразного эксперимента по применению универсального Принципа Полярности для создания естественной основы геометрии, страница 9

 

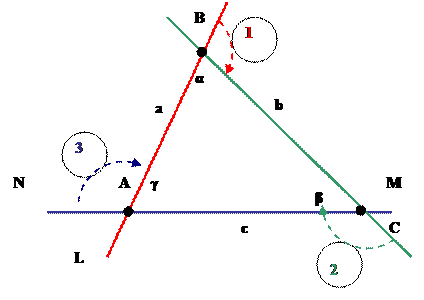
Рис. 9

Следовательно, сумма углов 1 + 2 + 3 = 2π

Вместе с тем, с учетом неизменной величины развернутого угла, - π:

величина угла 1 = (π – α);

величина угла 2 = (π – β);

величина угла 3 = (π – γ).

Отсюда получим, что

1 + 2 + 3 = (π – α) + (π – β) + (π – γ) = 3π – (α + β + γ) = 2π

Значит, в итоге, сумма углов в треугольнике тождественна:

α + β + γ = π.

Параллельные прямые

π-(π-β)=β

B

M

A

N

C

(π-α)

β

α

(π-β)

L

(π-β)

Если в ходе построения треугольника, в результате второго (последнего) разделения прямой в точке, треугольник не образовался, то, значит, исходная и последняя прямая, являются параллельными (не пересекающимися или не имеющими общей точки), см. рис. 10.

 

Рис. 10

При этом, угловая величина, содержащаяся в образованной «открытой» П-образной фигуре, составляет – π, т.е. – является такой же, как и у необразовавшегося треугольника:

α + β = π.

Равенство накрест лежащих углов, является совершенно очевидным из самого построения, поскольку проистекает из основного свойства развернутого угла.

Равенство секущих углов проистекает из неизменной угловой величины, содержащейся в треугольнике, или из сведения точек B и C в одну, когда отсутствует разделение прямой (прямые L и N, - совпадут):

если α + β = π, то α = π – β и β = π – α.

Тетраэдр

Как только треугольник определил (проявил) собой образ плоскости, так сразу же появилась возможность еще одного вида разделения точки и прямой, - их одномоментное разделение.

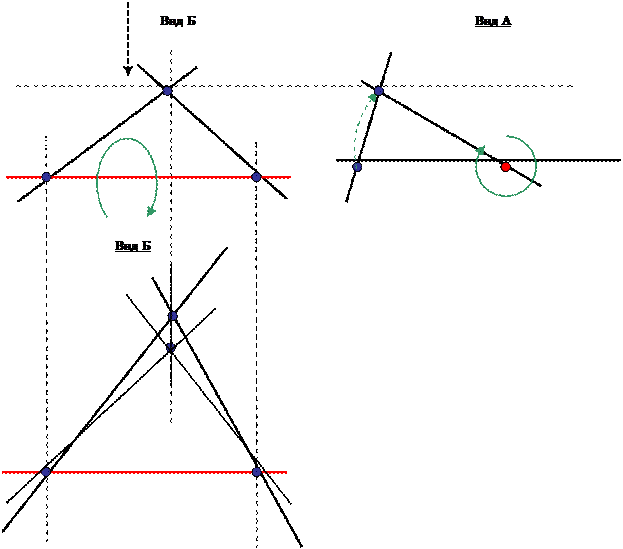
Иными словами, появилась возможность разделения особого вида, когда как бы происходит вращение прямой вокруг самой себя (вокруг своей оси), как точки (рис. 11):

 

Рис. 11

При этом происходит одномоментное разделение двух других линий и одной точки, не принадлежащих «вращающейся» линии.

Полученная фигура, в результате такого исключительного и последнего из всех возможных видов разделения, определяется, как тетраэдр (рис. 12).

 

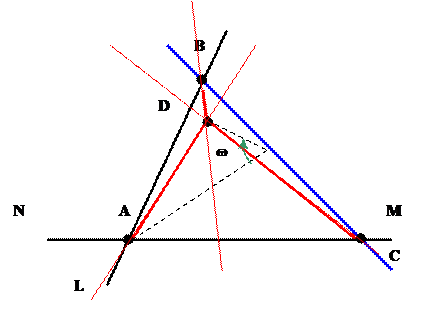Рис. 12

Тетраэдр воплощает собой трехмерность или объем (тело).

Таким образом, в результате настоящих исследований, были получены представления о пространствах различной мерности:

- ноль-мерное пространство, его образом является точка;

- одномерное пространство, его образом является отрезок;

- двухмерное пространство, его образом является треугольник;

- трехмерное пространство, его образом является тетраэдр.

Все эти результаты, наводят на довольно-таки интересное предположение

Дело в том, что мной рассмотрена полная группа всех возможных вариантов сочетаний двух основополагающих и противоположных, по сути своей, разделений первичных геометрических понятий – форм, - прямой и точки:

- разделение точки на прямой;

- разделение прямой в точке;

- минимально возможное последовательное разделение точки и прямой, заключающее в себе один полноценный цикл (окружность);

- одномоментное разделение точки и прямой в особой «прямой – точке».

Выходит, что наличие двух противоположностей (точки и прямой) в едином  основании геометрии (в линии или окружности), вполне естественным и необходимым образом приводит к определенной совокупности первичных геометрических образов – форм, таких, как:

- линия;

- окружность;

- прямая;

- точка;